题目内容
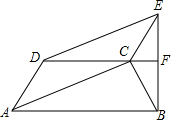如图，四边形ACED为平行四边形，DF垂直平分BE甲乙两虫同时从A点开始爬行到点F，甲虫沿着A-D-E-F的路线爬行，乙虫沿着A-C-B-F的路线爬行，若它们的爬行速度相同，则（ ）| A、甲虫先到 | B、乙虫先到 |
| C、两虫同时到 | D、无法确定 |
考点：平行四边形的判定与性质
专题：
分析：根据平行四边形的对边相等，以及线段的垂直平分线的性质，线段的垂直平分线上的点到线段的两端的距离相等，即可解答．
解答：解：∵四边形ABCD是平行四边形，
∴AD=CE，AC=DE，
又∵DF垂直平分BE，
∴CE=BC，EF=BF，
∴AD=BC，DE=AC，EF=BF．
∴AD+DE+EF=AC+BC+BF．
即甲虫沿着A-D-E-F的路线爬行，乙虫沿着A-C-B-F的路线爬行，路程相等，则爬行速度相等，则两虫同时到．
故选C．
∴AD=CE，AC=DE，
又∵DF垂直平分BE，
∴CE=BC，EF=BF，
∴AD=BC，DE=AC，EF=BF．
∴AD+DE+EF=AC+BC+BF．
即甲虫沿着A-D-E-F的路线爬行，乙虫沿着A-C-B-F的路线爬行，路程相等，则爬行速度相等，则两虫同时到．
故选C．
点评：本题考查了平行四边形的性质以及线段的垂直平分线的性质，理解性质定理是关键．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
某种鲸鱼的体重约为1.36×105千克，关于这个近似数，下列说法正确的是（ ）
| A、精确到百分位 |
| B、精确到十分位 |
| C、精确到个位 |
| D、精确到千位 |
如图，是一个用四块形状和大小都一样的长方形纸板拼成的一个大正方形，中间空的部分是-个小正方形，已知长方形纸板的长为m，宽为n（m＞n），则中间空的部分（小正方形）的面积是
如图所示，已知点O是∠ABC，∠ACB的平分线的交点，且OD∥AB，OE∥AC．