如图所示.将四张全等的长方形硬纸片围成一个正方形.根据图形阴影部分面积的关系.可以直观地得到一个关于a.b的恒等式为( ) A.a2-b2=B.(a+b)2=a2+2ab+b2C.(a-b)2=(a+b)2-4abD.a2+ab=a(a+b) 题目和参考答案——青夏教育精英家教网—

题目内容

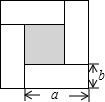如图所示，将四张全等的长方形硬纸片围成一个正方形，根据图形阴影部分面积的关系，可以直观地得到一个关于a、b的恒等式为（　　）

A、a²-b²=（a+b）（a-b）

B、（a+b）²=a²+2ab+b²

C、（a-b）²=（a+b）²-4ab

D、a²+ab=a（a+b）

考点：完全平方公式的几何背景

专题：

分析：用两种方法正确的表示出阴影部分的面积，再根据图形阴影部分面积的关系，即可直观地得到一个关于a、b的恒等式．

解答：解：方法一阴影部分的面积为：（a-b）²，
方法二阴影部分的面积为：（a+b）²-4ab，
所以根据图形阴影部分面积的关系，可以直观地得到一个关于a、b的恒等式为（a-b）²=（a+b）²-4ab．
故选：C．

点评：本题主要考查了完全平方公式的几何背景，解题的关键是用两种方法正确的表示出阴影部分的面积．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程y₁，y₂（千米）与行驶时间x（小时）之间的函数关系图象．

（1）填空：A，B两地相距

千米；货车的速度是

千米/时．
（2）求两小时后，货车离C站的路程y₂与行驶时间x之间的函数表达式；
（3）客、货两车何时相遇？

如图所示，已知点O是∠ABC，∠ACB的平分线的交点，且OD∥AB，OE∥AC．
（1）图中共有几个等腰三角形？并选一个进行证明．
（2）试说明△ODE的周长与BC的关系．
（3）若BC=12cm，求△ODE的周长．

一副直角三角板（其中一个三角板的内角是45°，45°，90°，另一个是30°，60°，90°）
（1）如图①放置，AB⊥AD，∠CAE=

，BC与AD的位置关系是

；
（2）在（1）的基础上，再拿一个30°，60°，90°的直角三角板，如图②放置，将AC′边和AD边重合，AE是∠CAB′的角平分线吗，如果是，请加以说明，如果不是，请说明理由．
（3）根据（1）（2）的计算，请解决下列问题：如图③∠BAD=90°，∠BAC=∠FAD=20°，将一个45°，45°，90°直角三角板的一直角边与AD边重合，锐角顶点A与∠BAD的顶点重合，AE是∠CAF的角平分线吗？如果是，请加以说明，如果不是，请说明理由．
（4）如果将图③中的∠BAC=∠FAD=α（α是锐角），其它条件不变，那么（3）问中的结论还成立吗？只需回答是还是不是，不需要说明理由．

3	10

某旅馆有客房120间，每间房的日租金为160元，每天都客满．旅馆装修后要提高租金，经市场调查，如果一间客房日租金每增加10元，则客房每天少出租6间，不考虑其他因素，旅馆将每间客房的日租金提高到多少元时，客房日租金的总收入最高？比装修前日租金的总收入增加多少元？

试题分类