题目内容
15．已知M=$\frac{（a-b）^{2}+4ab}{ab（a+b）^{2}}$（a，b≠0且a≠b）（1）化简M；
（2）若点P（a，b）在反比例函数y=$\frac{6}{x}$的图象上，求M的值．
分析 （1）根据完全平方公式先因式分解，再约分即可；
（2）根据题意得出ab=6，再计算得出M即可．
解答 解：（1）M=$\frac{（a-b）^{2}+4ab}{ab（a+b）^{2}}$=$\frac{（a+b）^{2}}{ab（a+b）^{2}}$=$\frac{1}{ab}$；
（2）∵点P（a，b）在反比例函数y=$\frac{6}{x}$的图象上，
∴ab=6，
∴M=$\frac{1}{ab}$=$\frac{1}{6}$．
点评 本题考查了反比例函数图象上点的坐标特征，掌握因式分解以及反比例函数的性质是解题的关键．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
5．下列各数中，最小的数是（ ）
| A． | （-3-2）3 | B． | （-3）（-2）3 | C． | （-3）2+（-2）3 | D． | （-3）3（-2）3 |
10．给出下列说法：
（1）两条直线被第三条直线所截，同位角相等；
（2）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；
（3）过一点有且只有一条直线与已知直线平行；
（4）从直线外一点到这条直线的垂线段，叫做这点到直线的距离；
（5）不相交的两条直线叫做平行线．
其中真命题有（ ）
（1）两条直线被第三条直线所截，同位角相等；
（2）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；
（3）过一点有且只有一条直线与已知直线平行；
（4）从直线外一点到这条直线的垂线段，叫做这点到直线的距离；
（5）不相交的两条直线叫做平行线．
其中真命题有（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
20．已知甲、乙两种原料中均含有A元素，其含量及每吨原料的购买单价如表所示：
已知用甲原料提取每千克A元素要排放废气1吨，用乙原料提取每千克A元素要排放废气0.5吨，若某厂要提取A元素20千克，并要求废气排放不超过16吨，则乙种原料最少需要多少吨？当乙种原料使用最少时，购买两种原料的费用是多少？
| A元素含量 | 单价（万元/吨） | |
| 甲原料 | 5% | 2.5 |
| 乙原料 | 8% | 6 |
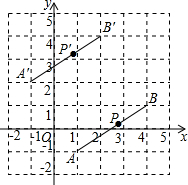如图，线段AB经过平移得到线段A′B′，其中点A，B的对应点分别为点A′，B′，这四个点都在格点上，若线段AB上有一个点P（a，b），则点P在A′B′上的对应点P′的坐标为（a-2，b+3）．
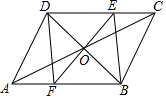在一次数学课上，张老师出示了一个题目：“如图，?ABCD的对角线相交于点O，过点O作EF垂直于BD交AB，CD分别于点F，E，连接DF，BE．请根据上述条件，写出一个正确结论．”其中四位同学写出的结论如下：