题目内容
14.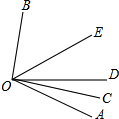 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线.(1)如果∠AOB=130°,求∠COE的度数.
(2)如果∠AOB=130°,∠COD=20°,求∠BOE的度数.
分析 (1)直接根据角平分线的定义进行解答即可;
(2)先根据∠COD=20°求出∠AOD的度数,再根据∠AOB=130°求出∠BOD的度数,根据角平分线的定义即可得出结论.
解答 解:(1)∵OC是∠AOD的平分线,OE是∠BOD的平分线,∠AOB=130°
∴∠COE=$\frac{1}{2}$∠BOD+$\frac{1}{2}$∠AOD
=$\frac{1}{2}$(∠BOD+∠AOD)
=$\frac{1}{2}$∠AOB
=65°;
(2)∵∠COD=20°,
∴∠AOD=2×20°=40°,
∵∠AOB=130°,
∴∠BOD=∠AOB-∠AOD=130°-40°=90°,
∵OE是∠BOD的平分线,
∴∠BOE=$\frac{1}{2}$∠BOD=$\frac{1}{2}$×90°=45°.
点评 本题考查的是角平分线的定义,熟知各角之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
相关题目
11.某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有( )
| A. | 103块 | B. | 104块 | C. | 105块 | D. | 106块 |
12.“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车去年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
4.在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为( )
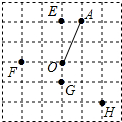

| A. | E、F、G | B. | F、G、H | C. | G、H、E | D. | H、E、F |
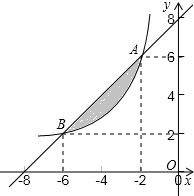 如图A、B两点在函数y=$\frac{k}{x}$(x<0)的图象上.
如图A、B两点在函数y=$\frac{k}{x}$(x<0)的图象上.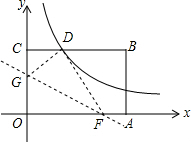 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.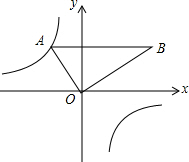 如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.