题目内容
15.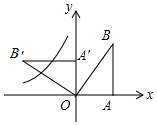 如图,在平面直角坐标系中,Rt△OAB的顶点A、B的坐标分别是(2,0),(2,4),将△OAB绕点O逆时针方向旋转90°,得到△OA′B′,函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,则k的值为( )
如图,在平面直角坐标系中,Rt△OAB的顶点A、B的坐标分别是(2,0),(2,4),将△OAB绕点O逆时针方向旋转90°,得到△OA′B′,函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,则k的值为( )| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
分析 根据旋转的性质,旋转不改变图形的大小和形状,所得图形与原图形全等求得A′的坐标(0,2),B′的坐标是(-4,2),进而求得中点C的坐标,然后根据待定系数法剪开求得k的值.
解答 解:∵点A、B的坐标分别是(2,0),(2,4),
∴OA=2,AB=4,
∵△A′B′O≌△ABO,
∵B(2,4),
∴A′的坐标为(0,2),B′的坐标是(-4,2)
∴A′B′的中点C(-2,2),
∵函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,
∴k=-2×2=-4,
故选B.
点评 本题考查了坐标与图形的变化-旋转,反比例函数图形上点的坐标特征,根据旋转的性质得出A′、B′的坐标是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
12.“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车去年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
20.在反比例函数y=$\frac{1-3k}{x}$的图象上有两点A(x1,y1),B(x2,y2),当0<x1<x2时,有y1>y2,则k的取值范围是( )
| A. | k$>\frac{1}{3}$ | B. | k$<\frac{1}{3}$ | C. | k$≥\frac{1}{3}$ | D. | k$≤\frac{1}{3}$ |
7.已知方程x-2y+3=8,则整式x-2y的值为( )
| A. | 5 | B. | 10 | C. | 12 | D. | 15 |
4.在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为( )
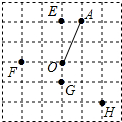

| A. | E、F、G | B. | F、G、H | C. | G、H、E | D. | H、E、F |
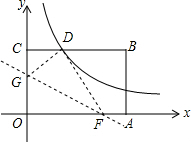 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.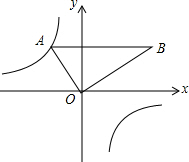 如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.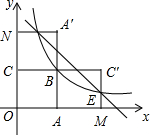 如图,四边形OABC是边长为2的正方形,函数y=$\frac{k}{x}(x>0)$的图象经过点B,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′,NA′BC.设线段MC′,NA′分别与函数y=$\frac{k}{x}(x>0)$的图象交于点E、F,则直线EF与x轴的交点坐标为(5,0).
如图,四边形OABC是边长为2的正方形,函数y=$\frac{k}{x}(x>0)$的图象经过点B,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′,NA′BC.设线段MC′,NA′分别与函数y=$\frac{k}{x}(x>0)$的图象交于点E、F,则直线EF与x轴的交点坐标为(5,0).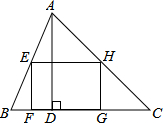 如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.
如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.