题目内容
 阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=| -1+2+3 |
| 3 |
| 4 |
| 3 |
|
(1)填空:min{
| 2 |
| 3 | 2 |
| 2 |
如果min{2,2x+2,4-2x}=2,则x的取值范围为
(2)①如果M{2,x+1,2x}=min{2,x+1,2x}=min{2,x+1,2x},求x;
②根据①,你发现了结论“如果M{a,b,c}=min{a,b,c},那么
③运用②的结论,填空:若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y}
,则x+y=
(3)在同一直角坐标系中作出函数y=x+1,y=(x-1)2,y=2-x的图象(不需列表描点).通过观察图象,
填空:min{x+1,(x-1)2,2-x}的最大值为
考点:二次函数综合题
专题:
分析:(1)因为用min(a,b,c)表示这三个数中最小的数,所以min{
,
,(
)0}就是括号内的三个数中最小的一个数,由
>
>(
)0,所以得出min{
,
,(
)0}=(
)0=1;由min{2,2x+2,4-2x}=2,得出2x+2≥2,且4-2x≥2,两个式子同时成立,据此即可求得x的范围;
(2)①M{2,x+1,2x}=
=x+1,若M{2,x+1,2x}=min{2,x+1,2x},则x+1是2、x+1、2x中最小的一个,即:x+1≤2且x+1≤2x,据此即可求得x的值;
②根据①可以得到结论:当三个数的平均数等于三个数中的最小的数,则这几个数相等,据此即可写出;
③根据结论,三个数相等,即可求得x,y的值,从而求得x+y的值;
(3)根据二次函数图象与一次函数图象的作法作出图象,然后根据min的定义解答即可.
| 2 |
| 3 | 2 |
| 2 |
| 2 |
| 3 | 2 |
| 2 |
| 2 |
| 3 | 2 |
| 2 |
| 2 |
(2)①M{2,x+1,2x}=
| 2+x+1+2x |
| 3 |
②根据①可以得到结论:当三个数的平均数等于三个数中的最小的数,则这几个数相等,据此即可写出;
③根据结论,三个数相等,即可求得x,y的值,从而求得x+y的值;
(3)根据二次函数图象与一次函数图象的作法作出图象,然后根据min的定义解答即可.
解答:解:(1)min{
,
,(
)0}=(
)0=1,
如果min{2,2x+2,4-2x}=2,则x的取值范围为0≤x≤1;
(2)①∵M{2,x+1,2x}=
=x+1,
∴2x-(x+1)=x-1.
当x≥1时,则min{2,x+1,2x}=2,则x+1=2,x=1.
当x<1时,则min{2,x+1,2x}=2x,则x+1=2x,x=1(舍去).
综上所述:x=1.
②a=b=c.理由如下:
∵M{a,b,c}=
,
如果min{a,b,c}=c,则a≥c,b≥c.
则有
=c,即a+b-2c=0,
∴(a-c)+(b-c)=0.
又∵a-c≥0,b-c≥0,
∴a-c=0且b-c=0.
∴a=b=c.
 其他情况同理可证,故a=b=c.
其他情况同理可证,故a=b=c.
③由②的结论,若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},
则2x+y+2=x+2y=2x-y,解得x=-3,y=-1,
所以x+y=-3-1=-4;
(3)作出图象,由图可知min{x+1,(x-1)2,2-x}的最大值为1.
故答案为1,0,1;a=b=c;-4;1.
| 2 |
| 3 | 2 |
| 2 |
| 2 |
如果min{2,2x+2,4-2x}=2,则x的取值范围为0≤x≤1;
(2)①∵M{2,x+1,2x}=
| 2+x+1+2x |
| 3 |
∴2x-(x+1)=x-1.
当x≥1时,则min{2,x+1,2x}=2,则x+1=2,x=1.
当x<1时,则min{2,x+1,2x}=2x,则x+1=2x,x=1(舍去).
综上所述:x=1.
②a=b=c.理由如下:
∵M{a,b,c}=
| a+b+c |
| 3 |
如果min{a,b,c}=c,则a≥c,b≥c.
则有
| a+b+c |
| 3 |
∴(a-c)+(b-c)=0.
又∵a-c≥0,b-c≥0,
∴a-c=0且b-c=0.
∴a=b=c.
 其他情况同理可证,故a=b=c.
其他情况同理可证,故a=b=c.③由②的结论,若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},
则2x+y+2=x+2y=2x-y,解得x=-3,y=-1,
所以x+y=-3-1=-4;
(3)作出图象,由图可知min{x+1,(x-1)2,2-x}的最大值为1.
故答案为1,0,1;a=b=c;-4;1.
点评:本题是二次函数的综合题,考查了一次函数、二次函数的图象与性质,比较大小以及利用已知提供信息得出函数值的方法,此题综合性较强,读懂题目信息并理解新定义“M”与“min”的意义是解题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
A、单项式
| ||||
| B、-3x2y+4x-1是三次三项式,常数项是1 | ||||
| C、单项式a的系数是0,次数是0 | ||||
D、单项式-
|

 已知二次函数y=-x2+4x-2.
已知二次函数y=-x2+4x-2.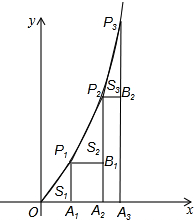 如图,已知A1,A2,A3…,A2008是x轴上的点,且OA1=A1A2=A2A3=…=A2007A2008=1,分别过点A1,A2,A3,…A2008作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3…,P2008点,若记△OA1P1的面积S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2007B2007P2008的面积为S2008,则S2008-S2007=
如图,已知A1,A2,A3…,A2008是x轴上的点,且OA1=A1A2=A2A3=…=A2007A2008=1,分别过点A1,A2,A3,…A2008作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3…,P2008点,若记△OA1P1的面积S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2007B2007P2008的面积为S2008,则S2008-S2007= 如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,若S△ABC=12,则四边形BDFE的面积为
如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,若S△ABC=12,则四边形BDFE的面积为