题目内容
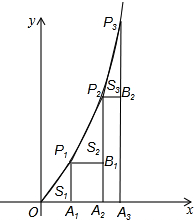 如图,已知A1,A2,A3…,A2008是x轴上的点,且OA1=A1A2=A2A3=…=A2007A2008=1,分别过点A1,A2,A3,…A2008作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3…,P2008点,若记△OA1P1的面积S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2007B2007P2008的面积为S2008,则S2008-S2007=
如图,已知A1,A2,A3…,A2008是x轴上的点,且OA1=A1A2=A2A3=…=A2007A2008=1,分别过点A1,A2,A3,…A2008作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3…,P2008点,若记△OA1P1的面积S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2007B2007P2008的面积为S2008,则S2008-S2007=考点:二次函数综合题
专题:
分析:把x=2008,x=2007及x=2006代入二次函数y=x2,即可求出三角形的边长,利用三角形的面积公式可求出S2007与S2008的值,即可得到结果.
解答:解:∵二次函数y=x2(x>0),OA1=A1A2=A2A3=…=A2007A2008=1,
∴当x=2008时,y=20082,
当x=2007时,y=20072,
当x=200时,y=20062.
∴S2007=
×1×(20072-20062)=
,
S2008=
×1×(20082-20072)=
,
∴S2008-S2007=1,
故答案为:1.
∴当x=2008时,y=20082,
当x=2007时,y=20072,
当x=200时,y=20062.
∴S2007=
| 1 |
| 2 |
| 4013 |
| 2 |
S2008=
| 1 |
| 2 |
| 4015 |
| 2 |
∴S2008-S2007=1,
故答案为:1.
点评:本题主要考查了二次函数综合题,解题的关键是求出三角形的边长.

练习册系列答案
相关题目
 阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=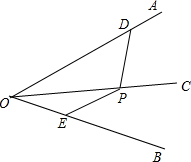 如图,OC平分∠AOB,点D,E分别在OA,OB上,点P在OC上且有PD=PE.求证:∠PDO=∠PEB.
如图,OC平分∠AOB,点D,E分别在OA,OB上,点P在OC上且有PD=PE.求证:∠PDO=∠PEB.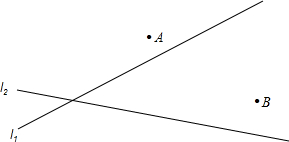 有公路l2同侧、l1异侧的两个城镇A、B,如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)
有公路l2同侧、l1异侧的两个城镇A、B,如图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路l1、l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)