题目内容
1.计算:(1)$\sqrt{\frac{25}{121}}$
(2)-$\sqrt{1{0}^{-4}}$
(3)$\frac{\sqrt{50}×\sqrt{32}}{\sqrt{8}}$-4
(4)$\frac{2\sqrt{12}+\sqrt{3}}{\sqrt{3}}$+(1-$\sqrt{3}$)0.
(5)(2$\sqrt{3}$+$\sqrt{6}$)(2$\sqrt{3}$-$\sqrt{6}$)
(6)$\sqrt{48}$÷$\sqrt{3}$+$\sqrt{\frac{1}{2}}$×$\sqrt{12}$-$\sqrt{24}$.
分析 (1)、(2)利用二次根式的性质化简;
(3)先把各二次根式化简为最简二次根式,然后约分即可;
(4)先把各二次根式化简为最简二次根式,然后利用二次根式的除法法则和零指数幂的意义计算;
(5)利用平方差公式计算;
(6)先根据二次根式的乘除法则运算,然后化简后合并即可.
解答 解:(1)原式=$\frac{5}{11}$;
(2)原式=-$\frac{1}{100}$;
(3)原式=$\frac{5\sqrt{2}×4\sqrt{2}}{2\sqrt{2}}$-4
=10$\sqrt{2}$-4;
(4)原式=$\frac{4\sqrt{3}+\sqrt{3}}{\sqrt{3}}$+1
=5+1
=6;
(5)原式=12-6
=6;
(6)原式=$\sqrt{48÷3}$+$\sqrt{\frac{1}{2}×12}$-2$\sqrt{6}$
=4+$\sqrt{6}$-2$\sqrt{6}$
=4-$\sqrt{6}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
6.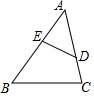 如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )
如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )
 如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )
如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )| A. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | B. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AC}$ |
 如图,AB=AC,BD=CE,用无刻度的直尺画出∠A的平分线.
如图,AB=AC,BD=CE,用无刻度的直尺画出∠A的平分线.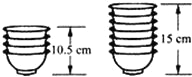 如图,两摞规格相同的碗整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题:
如图,两摞规格相同的碗整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题: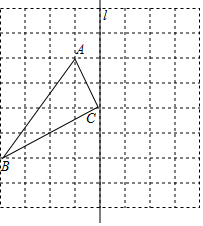 如图,在8×8的正方形网格中,每个小正方形的边长都是1,已知△ABC的三个顶点在格点上.
如图,在8×8的正方形网格中,每个小正方形的边长都是1,已知△ABC的三个顶点在格点上.