题目内容
6.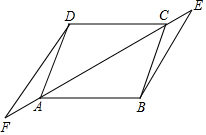 如图,?ABCD中,E,F是直线AC上两点,请在题目中添加合适的条件,就可以证明:BE=DF.
如图,?ABCD中,E,F是直线AC上两点,请在题目中添加合适的条件,就可以证明:BE=DF.(1)你添加的条件是AF=CE;
(2)请你根据题目中的条件和你添加的条件证明BE=DF.
分析 (1)利用平行四边形的性质借助全等三角形的判定与性质得出即可;
(2)利用全等三角形的性质结合平行线的判定方法得出即可.
解答 (1)解:添加AF=CE;
故答案为:AF=CE;
(2)证明∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAC=∠BCA,
∴∠DAF=∠BCE,
在△FAD和△ECB中,$\left\{\begin{array}{l}{AF=CE}&{\;}\\{∠FAD=∠ECB}&{\;}\\{AD=BC}&{\;}\end{array}\right.$,
∴△FAD≌△ECB(SAS),
∴BE=DF.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质,得出△FAD≌△ECB是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.用“>”“<”或“=”号填空:
| b>0 | b<0 | b=0 | |
| a>0 | ab>0 $\frac{b}{a}$>0 | ab<0 $\frac{b}{a}$<0 | ab=0 $\frac{b}{a}$=0 |
| a<0 | ab<0 $\frac{b}{a}$<0 | ab>0 $\frac{b}{a}$>0 | ab=0 $\frac{b}{a}$=0 |
5.已知△ABC中AB边的长为8,则△ABC的周长可能为( )
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
 如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且AB=AC.
如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且AB=AC.