题目内容
如图，已知EF∥AD，∠1=∠2，∠BAC=68°，求∠AGD的度数．考点：平行线的判定与性质
专题：
分析：由EF与AD平行，利用两直线平行同位角相等得到一对角相等，再由已知角相等，等量代换得到一对内错角相等，利用内错角相等两直线平行得到DG与AB平行，利用两直线平行同旁内角互补即可求出所求角的度数．
解答：解：∵EF∥AD，
∴∠1=∠3，
又∵∠1=∠2，
∴∠2=∠3，
∴AB∥DG，
∴∠BAC+∠AGD=180°，
∵∠BAC=68°，
∴∠AGD=112°．
∴∠1=∠3，
又∵∠1=∠2，
∴∠2=∠3，
∴AB∥DG，
∴∠BAC+∠AGD=180°，
∵∠BAC=68°，
∴∠AGD=112°．
点评：此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．
练习册系列答案
相关题目
在平面直角坐标系中，已知线段AB的两个端点分别是A（-4，-1），B（1，1），将线段AB平移得到线段A′B′，若点A′的坐标为（-2，2），则点B′的坐标为（ ）
| A、（3，4） |
| B、（4，3） |
| C、（-1，-2） |
| D、（-2，-1） |
-4的相反数是（ ）
| A、4 | ||
| B、-4 | ||
C、
| ||
D、-
|
如图，将一张矩形纸片对折后再对折，然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（ ）| A、矩形 | B、平行四边形 |
| C、梯形 | D、菱形 |
在已知的数轴上，表示-2.75的点是 （ ）| A、点E | B、点F | C、点G | D、点H |
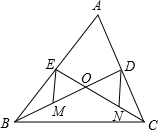如图，已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点．
如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F．
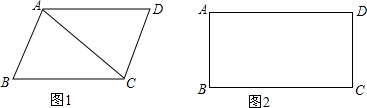
已知y是x的反比例函数，且当x=4，y=-1．