Question

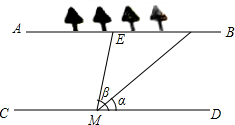小明所在小组要测量护城河的宽度，如图所示是护城河的一段，AB、CD是两岸（两岸平行），河岸AB上有一排树，相邻两棵树之间的距离均为10米（树粗忽略不计）．小明用测角仪在河岸CD的M处观测右数第一、四两棵树，观测线与CD所夹锐角分别为α、β．请你根据这些数据帮小明他们算出河宽（结果用含α、β的式子表示）．

Answer 1

考点：解直角三角形的应用

专题：

分析：设河宽为h米，分别过点E、K作EF⊥CD于点F，KG⊥CD于点G，由AB∥CD可知四边形EFGK是矩形，故EF=GK=h，再由FG=MG-MF即可得出结论．

解答：解：设河宽为h米，分别过点E、K作EF⊥CD于点F，KG⊥CD于点G，
∵AB∥CD可知四边形EFGK是矩形，
∴EF=GK=h，EK=FG=40米，
在Rt△EMF中，
∵

EF

MF

=tanβ，
∴MF=

EF

tanβ

=

h

tanβ

．
同理，在Rt△GKM中，MG=

h

tanα

．
∴FG=MG-MF=

h

tanβ

-

h

tanα

=40，
解得h=

40tanα•tanβ

tanα-tanβ

米．
答：河宽

40tanα•tanβ

tanα-tanβ

米．

点评：本题考查的是解直角三角形的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．