题目内容
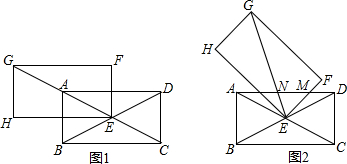
如图1,四边形ABCD、EFGH为两个全等的矩形,且矩形ABCD的对角线交于点E,点A在EG上,∠ACB=30°.将矩形EFGH绕点E顺时针旋转α角(0°<α<60°),如图2,GE、FE与AD分别相交于N、M.
(1)求证:AN+DM>MN;
(2)若MN2+DM2=AN2,求旋转角α的大小.
(1)求证:AN+DM>MN;
(2)若MN2+DM2=AN2,求旋转角α的大小.

考点:旋转的性质
专题:
分析:(1)根据矩形的对角线互相平分且相等可得AE=DE,再求出∠AED=120°,将△AEN绕点E顺时针旋转120°得到△DPE,连接MP,根据旋转的性质可得EP=NE,DP=AN,∠DEP=∠EN,再求出∠MEN=∠MEP=60°,然后利用“边角边”证明△MEN和△MEP全等,根据全等三角形对应边相等可得MN=MP,然后利用三角形的任意两边之和大于第三边证明即可;
(2)利用勾股定理逆定理判断出△DPM是直角三角形,根据全等三角形对应角相等可得∠EMN=∠EMP=45°,利用三角形的内角和定理求出∠MNE=75°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEN=45°,即为旋转角度数.
(2)利用勾股定理逆定理判断出△DPM是直角三角形,根据全等三角形对应角相等可得∠EMN=∠EMP=45°,利用三角形的内角和定理求出∠MNE=75°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEN=45°,即为旋转角度数.
解答:(1)证明:∵四边形ABCD是矩形,
∴AE=DE,
∵∠ACB=30°,
∴∠AED=180°-30°×2=120°,
将△AEN绕点E顺时针旋转120°得到△DPE,连接MP,
则EP=NE,DP=AN,∠DEP=∠EN,
∵∠AED=120°,
∴∠MEN=∠MEP=60°,
在△MEN和△MEP中,
,
∴△MEN≌△MEP(SAS),
∴MN=MP,
由三角形的三边关系得,DP+DM>MP,
∴AN+DM>MN;
(2)解:∵MN2+DM2=AN2,
∴△DPM是直角三角形,∠DMP=90°,
∵△MEN≌△MEP,
∴∠EMN=∠EMP=45°,
在△MNE中,∠MNE=180°-45°-60°=75°,
在△ANE中,∠AEN=∠MNE-∠CAD=75°-30°=45°,
∴旋转角为45°.
∴AE=DE,
∵∠ACB=30°,
∴∠AED=180°-30°×2=120°,
将△AEN绕点E顺时针旋转120°得到△DPE,连接MP,
则EP=NE,DP=AN,∠DEP=∠EN,
∵∠AED=120°,

∴∠MEN=∠MEP=60°,
在△MEN和△MEP中,
|
∴△MEN≌△MEP(SAS),
∴MN=MP,
由三角形的三边关系得,DP+DM>MP,
∴AN+DM>MN;
(2)解:∵MN2+DM2=AN2,
∴△DPM是直角三角形,∠DMP=90°,
∵△MEN≌△MEP,
∴∠EMN=∠EMP=45°,
在△MNE中,∠MNE=180°-45°-60°=75°,
在△ANE中,∠AEN=∠MNE-∠CAD=75°-30°=45°,
∴旋转角为45°.
点评:本题考查了旋转的性质,全等三角形的判定与性质,三角形的三边关系,勾股定理逆定理的应用,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图,AB是⊙O的直径,AM和BN是它的两条切线,CD切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.
如图,AB是⊙O的直径,AM和BN是它的两条切线,CD切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.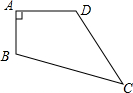 如图四边形ABCD,已知∠A=90°,AB=3,BC=13,CD=12,DA=4.求四边形的面积.
如图四边形ABCD,已知∠A=90°,AB=3,BC=13,CD=12,DA=4.求四边形的面积.