Question

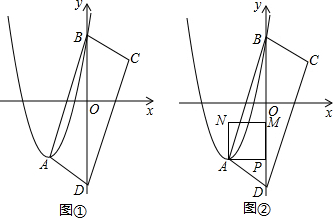
18．如图①，在平面直角坐标系中，抛物线y=x²-2mx+m²+$\frac{4}{3}$m的顶点为A，与y轴交于点B．当抛物线不经过坐标原点时，分别作点A、B关于原点的对称点C、D，连结AB、BC、CD、DA．
（1）分别用含有m的代数式表示点A、B的坐标．
（2）判断点B能否落在y轴负半轴上，并说明理由．
（3）连结AC，设l=AC+BD，求l与m之间的函数关系式．
（4）过点A作y轴的垂线，交y轴于点P，以AP为边作正方形APMN，MN在AP上方，如图②，当正方形APMN与四边形ABCD重叠部分图形为四边形时，直接写出m的取值范围．

Answer 1

分析 （1）根据配方法，可得顶点坐标，根据自变量与函数值得对应关系，可得B点坐标，
（2）根据B点的纵坐标小于零，可得不等式，根据解不等式，可得答案；
（3）根据平行四边形的性质，可得答案；
（4）根据正方形的边长小于BP，可得不等式，根据解不等式，可得答案．

解答 解：（1）配方，得
y=（x-m）²+$\frac{4}{3}$m，顶点A的坐标为（m，$\frac{4}{3}$m）
当x=0时，y=m²+$\frac{4}{3}$m，B点坐标为（0，m²+$\frac{4}{3}$m）

（2）点B能落在y轴负半轴上，理由如下：
由顶点坐标，得m＜0，
B点的纵坐标小于零，得
m²+$\frac{4}{3}$m=m（m+$\frac{4}{3}$）＜0，
由m＜0，得
m+$\frac{4}{3}$＞0，
得-$\frac{4}{3}$＜m＜0，
当-$\frac{4}{3}$＜m＜0时，点B能落在y轴负半轴上；

（3）OB=m²+$\frac{4}{3}$m，OA=-$\frac{5}{3}$m，
l=AC+BD=2OB+2OA=2（m²+$\frac{4}{3}$m）+2×（-$\frac{5}{3}$m）
即l=2m²-$\frac{2}{3}$m；

（4）由题意，得
AP＜BP，
即-m＜m²+$\frac{4}{3}$m-$\frac{4}{3}$m
解得m（m+1）＞0，
由m＜0，得m＞-1，
当-1＜m＜0时，AP＜BP，
正方形APMN与四边形ABCD重叠部分图形为四边形时，m的范围是-1＜m＜0．

点评 本题考查了二次函数综合题，解（1）的关键是配方法；解（2）的关键是解不等式；解（3）的关键是利用平行四边形的性质得出AC+BD=2OB+2OA；解（4）的关键是由四边形得出AP＜BP．