题目内容
7．下列因式分解正确的是（ ）| A． | 9-b2=（3-b）（3+b） | B． | x2-1=（1+x）（1-x） | C． | a2-2a+2=（a-1）2+1 | D． | 4a2-8a=2a（2a-4） |
分析 A、原式利用平方差公式分解得到结果，即可作出判断；
B、原式利用平方差公式分解得到结果，即可作出判断；
C、原式不能分解，错误；
D、原式提取公因式得到结果，即可作出判断．
解答 解：A、原式=（3+b）（3-b），正确；
B、原式=（x+1）（x-1），错误；
C、原式不能分解，错误；
D、原式=4a（a-2），错误，
故选A
点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．下列等式：
①$\frac{-（a-b）}{c}=\frac{a-b}{c}$
②$\frac{-（a-b）}{c}=\frac{b-a}{c}$
③$\frac{-m-n}{m}=\frac{m-n}{m}$
④$\frac{-m-n}{-m}=\frac{m+n}{m}$
成立的是（ ）
①$\frac{-（a-b）}{c}=\frac{a-b}{c}$
②$\frac{-（a-b）}{c}=\frac{b-a}{c}$
③$\frac{-m-n}{m}=\frac{m-n}{m}$
④$\frac{-m-n}{-m}=\frac{m+n}{m}$
成立的是（ ）
| A． | ①② | B． | ③④ | C． | ①③ | D． | ②④ |
贵阳市某中学初一年级的学生参加军训，在一次野外生存训练中，教官将一包食品随意埋在如图所示的区域中（图中每个三角形的大小、形状完全相同）．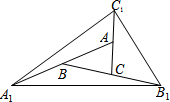
如图，△ABC面积为1，第一次操作：分别延长AB，BC，CA至点A1，B1，C1，使A1B=AB，B1C=BC，C1A=CA，顺次连接A1，B1，C1，得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2，B2，C2，得到△A2B2C2，那么△A2B2C2的面积是（ ）
如图，将Rt△ABC沿BC方向平移得到△DEF，其中∠ABC=90°，AB=6，BC=8，S△MEC=$\frac{8}{3}$，则BE=$\frac{16}{3}$．
16．在长为2、3、4、5的四根木条中，任选三根能组成三角形的选法有（ ）
| A． | 1种 | B． | 2种 | C． | 3种 | D． | 4种 |
△ABC沿x轴正方向平移7个单位长度至△DEF的位置，相应的坐标如图所示