题目内容
1.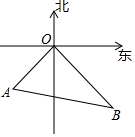 如图,甲轮船以24海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地以18海里/小时的速度向西南方向航行,已知他们离开港口半小时后分别到达B,A两地,求A,B两地之间的距离.
如图,甲轮船以24海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地以18海里/小时的速度向西南方向航行,已知他们离开港口半小时后分别到达B,A两地,求A,B两地之间的距离.
分析 根据题意可知∠AOB=90°,再由勾股定理即可得出结论.
解答 解:∵由题意可知∠AOB=90°,OA=9海里,OB=12海里,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15(海里).
答:A,B两地之间的距离是15海里.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
16.在Rt△ABC中,∠C=90°,a=6cm,b=8cm,则c的长是( )
| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
6.对于实数a,b,先定义一种新运算“★”如下:当a≥b时,a★b=a2+ab;当a<b时,a★b=b2+ab;若2★m=24,则实数m等于( )
| A. | 10 | B. | 4 | C. | 4或-6 | D. | 4或-6或10 |
11.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{10}$ | C. | $\sqrt{20}$ | D. | $\sqrt{\frac{1}{3}}$ |
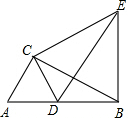 如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△CDE,使得点D恰好落在AB上,连接BE,则BE的长度为$\sqrt{3}$.
如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△CDE,使得点D恰好落在AB上,连接BE,则BE的长度为$\sqrt{3}$.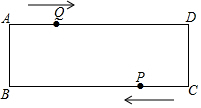 如图,在矩形ABCD中,AB=1cm,AD=3cm,点Q从A点出发,以1cm/s的速度沿AD向终点D运动,点P从点C出发,以1cm/s的速度沿CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动,两点同时出发,运动了t秒.
如图,在矩形ABCD中,AB=1cm,AD=3cm,点Q从A点出发,以1cm/s的速度沿AD向终点D运动,点P从点C出发,以1cm/s的速度沿CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动,两点同时出发,运动了t秒. 如图,在?ABCD中,已知AD=6cm,AB=4cm,AE平分∠BAD交BC边于点E,则EC=2cm.
如图,在?ABCD中,已知AD=6cm,AB=4cm,AE平分∠BAD交BC边于点E,则EC=2cm.