题目内容
9.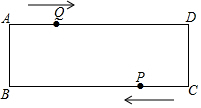 如图,在矩形ABCD中,AB=1cm,AD=3cm,点Q从A点出发,以1cm/s的速度沿AD向终点D运动,点P从点C出发,以1cm/s的速度沿CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动,两点同时出发,运动了t秒.
如图,在矩形ABCD中,AB=1cm,AD=3cm,点Q从A点出发,以1cm/s的速度沿AD向终点D运动,点P从点C出发,以1cm/s的速度沿CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动,两点同时出发,运动了t秒.(1)当0<t<3,判断四边形BQDP的形状,并说明理由;
(2)求四边形BQDP的面积S与运动时间t的函数关系式;
(3)求当t为何值时,四边形BQDP为菱形.
分析 (1)先判断出AD∥BC,AD=BC=3,再由运动知,AQ=PC=t,即可得出结论;
(2)利用平行四边形的面积公式即可得出结论;
(3)利用勾股定理表示出BQ,再由BQ=BP建立方程求解即可得出结论.
解答 解:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=3,
由运动知,AQ=t,PC=t,
∴AQ=PC,
∴AD-AQ=BC-PC,
∴DQ=BP,
∵AD∥BC,
∴四边形BQDP为平行四边形,
(2)由(1)知,四边形BQDP是平行四边形,
∵PC=t,
∴BP=BC-PC=3-t,
∴S=BP×AB=(3-t)×1=-t+3
(3)如图,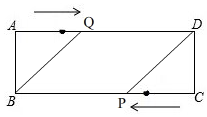
在Rt△ABQ中,AQ=t,AB=1,
根据勾股定理得,BQ=$\sqrt{A{Q}^{2}+A{B}^{2}}$=$\sqrt{{t}^{2}+1}$,
由运动知,CP=t,
∴BP=3-t,
∵平行四边形BQDP是菱形,
∴BQ=BP,
∴$\sqrt{{t}^{2}+1}$=3-t,
∴t=$\frac{4}{3}$,
当$t=\frac{4}{3}s$时,四边形BQDP为菱形.
点评 此题是四边形综合题,主要考查了矩形的性质,平行四边形的判定和性质,菱形的性质,解(1)的关键是得出AQ=PC,解(2)的关键是利用平行四边形的面积公式求解,解(3)的关键是表示出BQ,用BQ=BP建立方程求解,是一道中等难度的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.今年我市有1万名考生参加中考,为了了解这些考生的数学成绩,从中抽取500名考生的数学成绩进行统计分析,在这个问题中,下列说法:①这1万名考生的中考数学成绩的全体是总体;②每个考生是个体;③500名考生是总体的一个样本;④样本容量是500.其中说法正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.下列各式中,满足完全平方公式进行因式分解的是( )
| A. | 4x2-12xy+9y2 | B. | 2x2+4x+1 | C. | 2x2+4xy+y2 | D. | x2-y2+2xy |
18.下列调查中,适合采用全面调查(普查)方式的是( )
| A. | 对长江水质量情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某班45名学生身高情况的调查 | |
| D. | 对某批灯泡的使用寿命的调查 |
19.下列数据中,不能作为直角三角形三边长的是( )
| A. | 7、24、25 | B. | 6、8、10 | C. | 9、12、15 | D. | 5、12、15 |
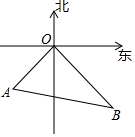 如图,甲轮船以24海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地以18海里/小时的速度向西南方向航行,已知他们离开港口半小时后分别到达B,A两地,求A,B两地之间的距离.
如图,甲轮船以24海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地以18海里/小时的速度向西南方向航行,已知他们离开港口半小时后分别到达B,A两地,求A,B两地之间的距离.