Question

5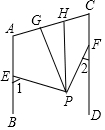．如图：AB∥CD，PG平分∠EPF，PH∥CD，下列结论：
①∠1+∠2=2∠EPG；   ②∠EPG-∠GPH=∠2；
③∠FPH=∠GPH；       ④设∠1＞∠2，则$\frac{∠1-∠2}{∠GPH}$为定值．
其中正确结论的个数是（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 根据AB∥CD，PH∥CD，可得AB∥CD∥PH，再根据平行线的性质以及角的和差关系进行计算，即可得出正确结论．

解答 解：∵AB∥CD，PH∥CD，
∴AB∥CD∥PH，
∴∠1=∠EPH，∠2=∠FPH，
∴∠1+∠2=∠EPF，
又∵PG平分∠EPF，
∴∠EPF=2∠EPG，故①正确；
∵∠2=∠FPH，∠EPG=∠FPG，
∴∠EPG-∠GPH=∠FPG-∠GPH=∠FPH=∠2，故②正确；
∵∠GPH与∠FPH不一定相等，
∴∠FPH=∠GPH不一定成立，故③错误；
∵∠1-∠2=∠EPH-∠FPH=（EPG+∠GPH）-∠FPH=∠FPG+∠GPH-∠FPH=∠GPH+∠GPH=2∠GPH，
∴$\frac{∠1-∠2}{∠GPH}$=2，为定值，故④正确．
故选：C．

点评 本题主要考查了平行线的性质以及角平分线的定义的运用，解题时注意：两直线平行，内错角相等．