题目内容
1.如图,△ABC中,AB=AC,AO是角平分线,D为AO上一点,作△CDE,使DE=DC,∠EDC=∠BAC,连接BE.
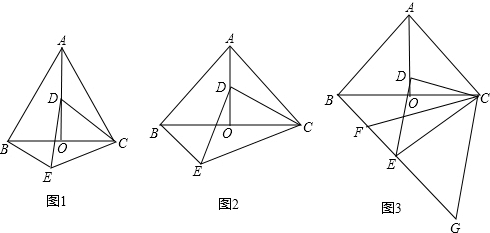
(1)若∠BAC=60°,求证:△ACD≌△BCE;
(2)若∠BAC=90°,AD=DO,求$\frac{BE}{BC}$的值;
(3)若∠BAC=90°,F为BE中点,G为 BE延长线上一点,CF=CG,AD=nDO,直接写出$\frac{BF}{FG}$的值.
分析 (1)只要证明∠ACD=∠BCE,即可根据SAS证得△ACD≌△BCE;
(2)首先证明△ACD∽△BCE,得$\frac{BE}{AD}$=$\frac{BC}{AC}$=$\sqrt{2}$,再根据AD=$\frac{1}{4}$BC即可解决问题.
(3)如图3中,作CH⊥BG于H.设OD=k,则AD=nk,BE=$\sqrt{2}$nk,AO=(n+1)k,首先证明△ABC≌△HBC,得BH=CH=AB=AC=$\sqrt{2}$(n+1)k,BF=$\frac{1}{2}$$\sqrt{2}$nk,求出BG即可解决问题.
解答 (1)证明:如图1中,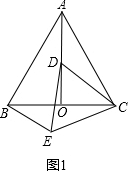
∵△ABC和△CDE为等边三角形,
∴AC=BC,CD=CE.∠ACB=∠DCE=60°,
∴∠ACB-∠DCO=∠DCE-∠DCO,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS);
(2)如图2中,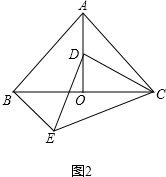
∵AB=AC,OA平分∠BAC,
∴AO⊥BC,OB=OC,
∵∠BAC=∠EDC=90°,AB=AC,DE=DC,
∴∠ACB=∠DCE=45°,BC=$\sqrt{2}$AC,EC=$\sqrt{2}$CD,
∴$\frac{BC}{AC}$=$\frac{EC}{CD}$,∠ACD=∠BCE,
∴△ACD∽△BCE,
∴$\frac{BE}{AD}$=$\frac{BC}{AC}$=$\sqrt{2}$,
∵OA=OB=OC,AD=OD,
∴AD=$\frac{1}{4}$BC,
∴$\frac{BE}{\frac{1}{4}BC}$=$\sqrt{2}$,
∴$\frac{BE}{BC}$=$\frac{\sqrt{2}}{4}$.
(3)如图3中,作CH⊥BG于H.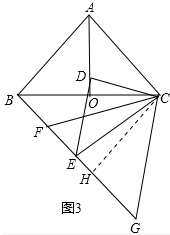
由(2)可知△ACD∽△BCE,
∴BE:AD=$\sqrt{2}$,∠CAD=∠CBE=45°,设OD=k,则AD=nk,BE=$\sqrt{2}$nk,AO=(n+1)k,
∵∠ABC=∠HBC=45°,∠BAC=∠BHC,BC=BC,
∴△ABC≌△HBC,
∴BH=CH=AB=AC=$\sqrt{2}$(n+1)k,BF=$\frac{1}{2}$$\sqrt{2}$nk,
FH=HG=$\sqrt{2}$(n+1)k-$\frac{1}{2}$$\sqrt{2}$nk,
∴$\frac{BF}{FG}$=$\frac{\frac{\sqrt{2}}{2}nk}{2[\sqrt{2}(n+1)k-\frac{\sqrt{2}}{2}nk]}$=$\frac{n}{2n+4}$.
点评 本题考查相似三角形综合题、等边三角形的性质、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是灵活应用这些知识解决问题,学会添加辅助线,构造全等三角形,学会利用参数解决问题,属于中考压轴题.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 如图,其主视图是( )
如图,其主视图是( )| A. |  | B. |  | C. |  | D. | 无法确定 |
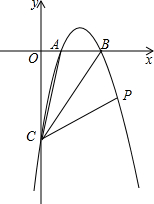 如图,抛物线y=-x2+3x-2与x轴交于A、B两点,与y轴交于C点,点P在抛物线上,∠ACB=∠BCP,求P点的坐标.
如图,抛物线y=-x2+3x-2与x轴交于A、B两点,与y轴交于C点,点P在抛物线上,∠ACB=∠BCP,求P点的坐标.