题目内容
7.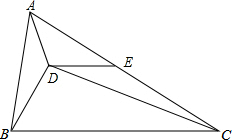 已知D是△ABC内一点,E是边AC的中点,AB=6,BC=10,∠BAD=∠BCD,∠EDC=∠ABD.求DE的长.
已知D是△ABC内一点,E是边AC的中点,AB=6,BC=10,∠BAD=∠BCD,∠EDC=∠ABD.求DE的长.
分析 延长CD到F、使CD=DF知DE∥AF、DE=$\frac{1}{2}$AF,通过∠ABD=∠DFA=∠EDC知点A、F、B、D四点共圆,从而得到∠BFD=∠BCD=∠BAD,证△BFD≌△BCD知∠BAF=∠BDF=90°,在RT△BAF中根据勾股定理可得AF的长即可.
解答 解:如图,延长CD到F,使CD=DF,连接AF、BF,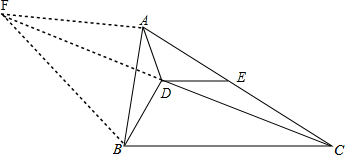
∵E是AC中点,CD=DF,
∴DE∥AF,且DE=$\frac{1}{2}$AF,
∴∠CDE=∠DFA,
∵∠EDC=∠ABD,
∴∠ABD=∠DFA=∠EDC,
∴点A、F、B、D四点共圆,
∴∠BAD=∠BFD,
又∵∠BAD=∠BCD,
∴∠BFD=∠BCD,
∴BF=BC,
在△BFD和△BCD中,
∵$\left\{\begin{array}{l}{BF=BC}\\{BD=BD}\\{DC=DF}\end{array}\right.$,
∴△BFD≌△BCD(SSS),
∴∠BDF=∠BDC=$\frac{1}{2}$∠CDF=90°,
∵点A、F、B、D四点共圆,
∴∠BAF=∠BDF=90°,
在RT△BAF中,∵BF=BC=10,AB=6,
∴AF=8,
∴DE=$\frac{1}{2}$AF=4.
点评 本题主要考查全等三角形的判定和性质,添加辅助线构造△BFD≌△BCD是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
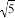 +1 B. -
+1 B. -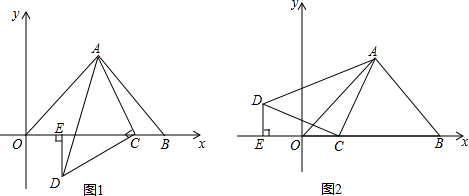

 已知:如图,∠1=∠2.
已知:如图,∠1=∠2.