题目内容
15.在直角坐标系中,点B在x轴上,OA=AB,∠OAB=90°,A(4,4),点C为线段OB上一动点,以每秒1个单位长度从点B出发向点O运动,当运动时间为t秒时,以AC为边作△ACD,∠ACD=90°,AC=CD,作DE⊥x轴于点E.(1)如图1,用含t的代数式表示线段OE的长;
(2)在图2中,用含t的代数式表示线段OE的长.
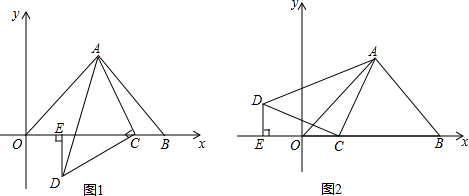
分析 (1)如图1中,作AM⊥OB垂足为M,只要证明△AMC≌△CED得AM=EC=4,利用线段和差定义即可解决.
(2)如图2中,作AM⊥OB垂足为M,只要证明△AMC≌△CED得AM=EC=4,利用线段和差定义即可解决.
解答 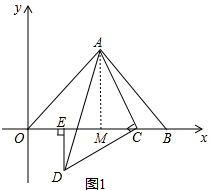 解;(1)如图1中,作AM⊥OB垂足为M.
解;(1)如图1中,作AM⊥OB垂足为M.
∵∠AMC=∠CED=∠ACD=90°,
∴∠ACM+∠DCE=90°,∠DCE+∠EDC=90°,
∴∠ACM=∠CDE,
在△AMC和△CED中,
$\left\{\begin{array}{l}{∠AMC=∠CED}\\{∠ACM=∠CDE}\\{AC=CD}\end{array}\right.$,
∴△AMC≌△CED,
∴AM=CE,
∵OA=AB,AM⊥OB,
∴AM=OM=MB=4,CE=AM=4,
∴OE=OB-EC-BC=8-4-t=4-t.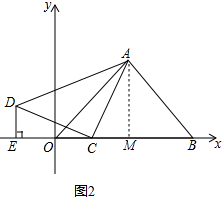
(2)如图2中,作AM⊥OB垂足为M.
∵∠AMC=∠CED=∠ACD=90°,
∴∠ACM+∠DCE=90°,∠DCE+∠EDC=90°,
∴∠ACM=∠CDE,
在△AMC和△CED中,
$\left\{\begin{array}{l}{∠AMC=∠CED}\\{∠ACM=∠CDE}\\{AC=CD}\end{array}\right.$,
∴△AMC≌△CED,
∴AM=CE,
∵OA=AB,AM⊥OB,
∴AM=OM=MB=4,CE=AM=4,
∴OE=EC-OC=EC-(OB-BC)=4-(8-t)=t+4.
点评 本题考查等腰三角形的性质、全等三角形的判定和性质、线段和差定义,添加辅助线寻找全等三角形是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.-3的绝对值是( )
| A. | 3 | B. | |-3| | C. | -3 | D. | ±3 |

 B. 2 C.
B. 2 C.  D. 2
D. 2 ,求
,求 的值.
的值. 在平面直角坐标系中,抛物线C1:y=$\frac{1}{2}{x}^{2}$,把C1沿x轴向右平移m(m>0)个单位长度,得抛物线C2,C1和C2的交点为点Q,顶点分别是O和P,
在平面直角坐标系中,抛物线C1:y=$\frac{1}{2}{x}^{2}$,把C1沿x轴向右平移m(m>0)个单位长度,得抛物线C2,C1和C2的交点为点Q,顶点分别是O和P, +
+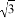 =
=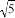 B. 4
B. 4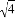 =1
=1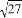 ÷
÷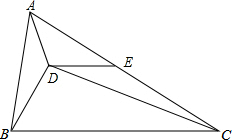 已知D是△ABC内一点,E是边AC的中点,AB=6,BC=10,∠BAD=∠BCD,∠EDC=∠ABD.求DE的长.
已知D是△ABC内一点,E是边AC的中点,AB=6,BC=10,∠BAD=∠BCD,∠EDC=∠ABD.求DE的长.