题目内容
2.在△ABC中 AB=AC,过点C作∠MCB=∠BAC,MC所在直线交AB所在直线于点D,过点D作CE⊥AC,垂足为点E.(1)如图①,求证:AD-AB=2CE;
(2)如图②,图③,线段AD,AB,CE又有怎样数量关系?请写出你的猜想,不需证明;
(3)填空:若AC=3,CE=2,则AD=7或1.

分析 (1)作DH∥BC交AE的延长线于H,先证明BD=HC,再证明HC=2CE即可解决.
(2)①结论AD+AB=2EC,作DH∥BC交CA的延长线于H,先证明BD=HC,再证明HC=2CE即可解决.
②结论AD+AB=2EC,作DH∥BC交CA的延长线于H,先证明BD=HC,再证明HC=2CE即可解决.
(3)利用图1、图2的结论计算即可,图3不合题意.
解答 (1)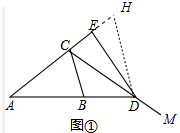 证明:如图1中,作DH∥BC交AE的延长线于H.
证明:如图1中,作DH∥BC交AE的延长线于H.
∵AC=AB,
∴∠ACB=∠ABC,
∵BC∥DH,
∴∠ACB=∠H,∠ABC=∠ADN,
∴∠H=∠ADH,
∴AD=AH,
∴BD=CH,
∵∠BCD=∠A,∠HCB=∠A+∠ABC,
∴∠HCB=∠ABC=∠H,
∴DC=DH,
∵DE⊥CH,
∴CE=EH,
∴HC=2EC,
∴AD-AB=BD=CH=2EC.
(2)①如图2中结论:AB+AD=2EC,理由如下: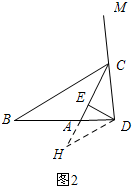 证明:作DH∥BC交CA的延长线于H.
证明:作DH∥BC交CA的延长线于H.
∵AC=AB,
∴∠ACB=∠ABC,
∵BC∥DH,
∴∠ACB=∠H,∠ABC=∠ADN,
∴∠H=∠ADH,
∴AD=AH,
∴BD=CH,
∵∠BCM+∠BCA+∠HCD=180°,∠BAC+∠B+∠BCA=180°,
∵∠BCM=∠BAC,
∴∠HCD=∠B=∠H,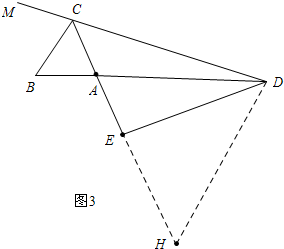
∴DC=DH,
∵DE⊥CH,
∴CE=EH,
∴HC=2EC,
∴AD-AB=BD=CH=2EC.
②如图3中,结论:AB+AD=2FC,理由如下:
作DH∥BC交CA的延长线于H.
∵AC=AB,
∴∠ACB=∠ABC,
∵BC∥DH,
∴∠ACB=∠H,∠ABC=∠ADN,
∴∠H=∠ADH,
∴AD=AH,
∴BD=CH,
∵∠BCM+∠BCA+∠HCD=180°,∠BAC+∠B+∠BCA=180°,
∵∠BCM=∠BAC,
∴∠HCD=∠B=∠H
∴DC=DH,
∵DE⊥CH,
∴CE=EH,
∴HC=2EC,
∴AD-AB=BD=CH=2EC.
(3)解:在图1中,∵AD-AB=2EC,AB=AC=3,EC=2,
∴AD-3=4
∴AD=7,
在图2中,∵AD+AB=2EC,AB=AC=3,CE=2,
∴AD+3=4,
∴AD=1,
在图3中,∵AC<CE不合题意.
故答案为7或1.
点评 本题考查等腰三角形性质、平行线的性质,通过作平行线构造等腰三角形是解决问题的关键.

| A. | -32=-6 | B. | (-3)2=6 | C. | -32=9 | D. | (-3)2=9 |
 (
( )的相反数是( ).
)的相反数是( ).
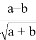 ,例如3※1=
,例如3※1=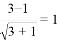 .那么8※12= ______ .
.那么8※12= ______ .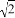 +
+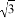 =
=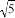 B. 4
B. 4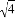 =1
=1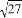 ÷
÷ 如图,四边形ABCD中,∠BAD=90°,对角线AC与BD相交于点O,BO=DO,点E、F分别是AD、AC的中点.
如图,四边形ABCD中,∠BAD=90°,对角线AC与BD相交于点O,BO=DO,点E、F分别是AD、AC的中点.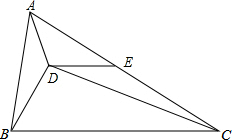 已知D是△ABC内一点,E是边AC的中点,AB=6,BC=10,∠BAD=∠BCD,∠EDC=∠ABD.求DE的长.
已知D是△ABC内一点,E是边AC的中点,AB=6,BC=10,∠BAD=∠BCD,∠EDC=∠ABD.求DE的长. 表示运算x+y+z,
表示运算x+y+z, 表示运算a-b-c+d,那么
表示运算a-b-c+d,那么  的结果是多少?
的结果是多少?