题目内容
5.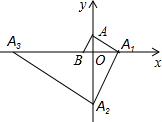 如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2017为止,则点A2017坐标为(31009,0).
如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2017为止,则点A2017坐标为(31009,0).
分析 分别写出A1、A2、A3的坐标找到变化规律后写出答案即可.
解答 解:∵A(0,$\sqrt{3}$)、B(-1,0),
∴AB⊥AA1,
∴A1的坐标为:(3,0),
同理可得:A2的坐标为:(0,-3$\sqrt{3}$),A3的坐标为:(-9,0),
…
∵2017÷4=504…1,
∴点A2017横坐标为${3}^{\frac{2017+1}{2}}$,即:31009,
点A2017坐标为(31009,0).
故答案为:(31009,0).
点评 本题考查了规律型问题,解题的关键是根据点的坐标的变化得到规律,利用得到的规律解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 如图,已知四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN是菱形.
如图,已知四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN是菱形.