题目内容
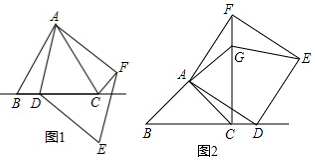
15.如图1是边长为6的菱形ABCD,E是BC的中点,AE、BD相交于点P.(1)如图2,当∠ABC=90°时,求BP的长.
(2)如图3,当∠ABC角度在改变时,BP的中垂线与边BC的交点F的位置是否发生变化?如果不变,请求出BF的长;如果改变,请说明理由.
(3)当∠ABC从90°逐步减少到30°的过程中,求P点经过路线长.

分析 (1)由菱形的性质得出AD=BC=CD=6,AD∥BC,由平行线得出△BEP∽△DAP,得出比例式$\frac{BP}{DP}=\frac{BE}{AD}$=$\frac{1}{2}$,证明菱形ABCD是正方形,由勾股定理得出BD=6$\sqrt{2}$,得出BP=$\frac{1}{3}$BD=2$\sqrt{2}$;
(2)由菱形的性质得出∠ABD=∠CBD,由垂直平分线的性质得出BF=PF,由等腰三角形的性质得出∠FBP=∠BPF,∠BPF=∠ABD,证出PF∥AB∥CD,得出比例式$\frac{BF}{BC}=\frac{BP}{BD}$=$\frac{1}{3}$,求出BF=$\frac{1}{3}$BC=2即可;
(3)P点经过路线是以F为圆心,BF为半径的圆弧,由弧长公式即可得出答案.
解答 解:(1)∵E是BC的中点,
∴BE=CE=$\frac{1}{2}$BC,
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∴△BEP∽△DAP,
∴$\frac{BP}{DP}=\frac{BE}{AD}$=$\frac{1}{2}$,
∵∠ABC=90°,
∴菱形ABCD是正方形,
∴BD=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$,
∴BP=$\frac{1}{3}$BD=2$\sqrt{2}$;
(2)不发生变化;理由如下:
∵四边形ABCD是菱形,
∴∠ABD=∠CBD,
又∵BP的中垂线与边BC交于点F,
∴BF=PF,
∴∠FBP=∠BPF,∠BPF=∠ABD,
∴PF∥AB∥CD,
∴$\frac{BF}{BC}=\frac{BP}{BD}$=$\frac{1}{3}$,
∴BF=$\frac{1}{3}$BC=2,
即点F的位置不发生改变;
(3)P点经过路线是以F为圆心,BF为半径的圆弧,长度为$\frac{(90-30)π×2}{180}$=$\frac{2}{3}$π.
点评 本题是四边形综合题目,考查了菱形的性质、正方形的判定与性质、相似三角形的判定与性质、勾股定理、线段垂直平分线的性质以及弧长公式等知识;熟练掌握菱形的性质,证明三角形相似是解决问题的关键.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案| A. | 40° | B. | 70° | C. | 55°或70° | D. | 40°或70° |
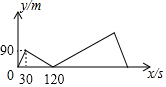 甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后$\frac{360}{7}$秒与甲相遇.
甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后$\frac{360}{7}$秒与甲相遇.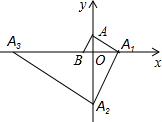 如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2017为止,则点A2017坐标为(31009,0).
如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2017为止,则点A2017坐标为(31009,0).