题目内容
3. 如图,在平面直角坐标系中,点A的坐标为(-2,2),点B与点A关于x轴对称,点B先向右平移4个单位长度,再向上平移2个单位长度得到点C.
如图,在平面直角坐标系中,点A的坐标为(-2,2),点B与点A关于x轴对称,点B先向右平移4个单位长度,再向上平移2个单位长度得到点C.(1)描出点B和点C,并依次连接AB、BC、CA,得到△ABC;
(2)先将(1)中的△ABC的各顶点的横坐标和纵坐标都乘$\frac{3}{2}$,得到点A的对应点A1,点B的对应点B1,点C的对应点C1,写出A1、B1、C1的坐标,并在平面直角坐标系中描出点A1、B1、C1,得到△A1B1C1.
分析 (1)由轴对称得点B坐标,将点B平移得点C,连接可得△ABC;
(2)将(1)中点A、B、C横坐标和纵坐标都乘$\frac{3}{2}$得点A1、B1、C1坐标,连接可得△A1B1C1.
解答 解:(1)如图,△ABC即为所求作三角形;
(2)由(1)知,点A(-2,2)、点B(-2,-2)、点C(2,0),
则点A1(-3,3)、点B1(-3,-3)、点C1(3,0),
如图,△A1B1C1即为所求作三角形.
点评 本题主要考查轴对称变换、平移变换、位似变换的作图,熟练掌握它们的定义是解题的根本.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
6.x取下列各数中的哪个数时,式子$\sqrt{x-3}$在实数范围内有意义( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
14.下列计算中,正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | D. | $\sqrt{(-3)^{2}}$=3 |
11.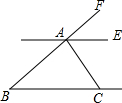 如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )
如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )
 如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )
如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )| A. | 50° | B. | 60° | C. | 40° | D. | 30° |
 如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2). 已知a、b、c在数轴上的位置如图,化简:|a|+|c-b|-|c|.
已知a、b、c在数轴上的位置如图,化简:|a|+|c-b|-|c|.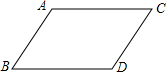 如图,将长为4cm的线段AB沿着点A到点C的方向平移6cm得到线段CD,那么四边形ABDC的周长是20cm.
如图,将长为4cm的线段AB沿着点A到点C的方向平移6cm得到线段CD,那么四边形ABDC的周长是20cm.