题目内容
1．n边形的内角和为1440°，则n=10．分析 根据n边形的内角和是（n-2）•180°，即可列方程求解．
解答 解：设此多边形的边数为n，由题意，有
（n-2）•180°=1440°，
解得n=10．
即此多边形的边数为10．
故答案为10．
点评 本题主要考查了多边形的内角和公式，是一个基础题，比较简单，牢记n边形的内角和公式是解题的关键．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
19．
如图，P为正方形ABCD对角线BD上一动点，若AB=2，则AP+BP+CP的最小值为（ ）
如图，P为正方形ABCD对角线BD上一动点，若AB=2，则AP+BP+CP的最小值为（ ）| A． | $\sqrt{2}$+$\sqrt{5}$ | B． | $\sqrt{2}$+$\sqrt{6}$ | C． | 4 | D． | 3$\sqrt{2}$ |
9．
实数a在数轴上的位置如图所示，则化简|1-a|+$\sqrt{（a-2）^{2}}$的结果是（ ）
实数a在数轴上的位置如图所示，则化简|1-a|+$\sqrt{（a-2）^{2}}$的结果是（ ）| A． | -1 | B． | 1 | C． | 2a-3 | D． | 3-2a |
16．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2016次运动后，动点P的坐标是（ ）
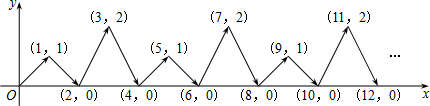
| A． | （2016，1） | B． | （2016，0） | C． | （2016，2） | D． | （2017，0） |
如图，在平面直角坐标系中，矩形AOCB扩大以点0为位似中心扩大1.5倍得到矩形DOFE，已知点B的坐标为（2，3），点E的坐标为（3，4.5）．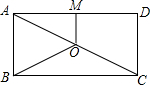
如图，O是矩形ABCD的对角线AC的中点，M是AD的中点．若OM=3，AD=8，则BO=5．