题目内容
11.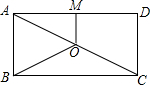 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若OM=3,AD=8,则BO=5.
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若OM=3,AD=8,则BO=5.
分析 已知OM是△ADC的中位线,再结合已知条件则DC的长可求出,所以利用勾股定理可求出AC的长,由直角三角形斜边上中线的性质则BO的长即可求出.
解答 解:∵四边形ABCD是矩形,
∴∠D=90°,
∵O是矩形ABCD的对角线AC的中点,M是AD的中点,
∴OM是△ADC的中位线,
∴OM=3,
∴DC=6,
∵AD=8,
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=10,
∴BO=$\frac{1}{2}$AC=5,
故答案为:5.
点评 本题考查了矩形的性质,勾股定理的运用,直角三角形斜边上中线的性质以及三角形的中位线的应用,解此题的关键是求出AC的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列各图象中,不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,小正方形的边长为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )



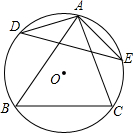 如图,△ABC内接于⊙O,∠BAC=60°,D、E分别为$\widehat{AB}$和$\widehat{AC}$的中点,连结DE.
如图,△ABC内接于⊙O,∠BAC=60°,D、E分别为$\widehat{AB}$和$\widehat{AC}$的中点,连结DE.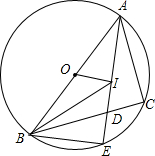 如图,△ABC内接于⊙O,AB是⊙O的直径,I是△ABC内一点,AI的延长线交BC于点D,交⊙O于E,连接BE,BI,若IB平分∠ABC,EB=EI.
如图,△ABC内接于⊙O,AB是⊙O的直径,I是△ABC内一点,AI的延长线交BC于点D,交⊙O于E,连接BE,BI,若IB平分∠ABC,EB=EI.