题目内容
10.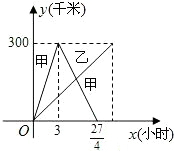 已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)它们出发$\frac{9}{2}$小时时,离各自出发地的距离相等,求乙车离出发地的距离y乙(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
分析 (1)由图知,该函数关系在不同的时间里表现成不同的关系,需分段表达.当行驶时间小于3时是正比例函数;当行使时间大于3小时小于$\frac{27}{4}$小时是一次函数.可根据待定系数法列方程,求函数关系式.
(2)4.5小时大于3小时,代入一次函数关系式,计算出乙车在用了$\frac{9}{2}$小时行使的距离.从图象可看出求乙车离出发地的距离y(千米)与行驶时间x(小时)之间是正比例函数关系,用待定系数法可求解.
(3)两者相向而行,相遇时甲、乙两车行使的距离之和为300千米,列出方程解答,由题意有两次相遇.
解答 解:(1)当0≤x≤3时,是正比例函数,设为y=kx,
x=3时,y=300,代入解得k=100,所以y=100x;
当3<x≤$\frac{27}{4}$时,是一次函数,设为y=kx+b,
代入两点(3,300)、($\frac{27}{4}$,0),得$\left\{\begin{array}{l}{3k+b=300}\\{\frac{27}{4}k+b=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-80}\\{b=540}\end{array}\right.$,
所以y=540-80x.
综合以上得甲车离出发地的距离y与行驶时间x之间的函数关系式 为:y=$\left\{\begin{array}{l}{100x(0≤x≤3)}\\{540-80x(3<x≤\frac{27}{4})}\end{array}\right.$.
(2)当x=$\frac{9}{2}$时,y甲=540-80×$\frac{9}{2}$=180;
乙车过点($\frac{9}{2}$,180),y乙=40x.(0≤x≤$\frac{15}{2}$)
(3)由题意有两次相遇.
①当0≤x≤3,100x+40x=300,解得x=$\frac{15}{7}$;
②当3<x≤$\frac{27}{4}$时,(540-80x)+40x=300,解得x=6.
综上所述,两车第一次相遇时间为第$\frac{15}{7}$小时,第二次相遇时间为第6小时.
点评 本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.此题中需注意的是相向而行时相遇的问题.

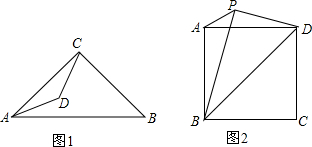
 如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形BCED的面积比为( )
如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形BCED的面积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 3:4 |
 一个正方体的表面展开图如图所示,则原正方体中“行”字所在的面相对的面上标的字是( )
一个正方体的表面展开图如图所示,则原正方体中“行”字所在的面相对的面上标的字是( )| A. | 步 | B. | 量 | C. | 青 | D. | 春 |
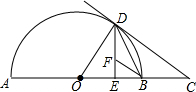 如图,AB是半圆O的直径,过半圆O上一点D作DE⊥AB,垂足为E,作半圆O的切线DC,交AB的延长线于点C,连结OD、BD.
如图,AB是半圆O的直径,过半圆O上一点D作DE⊥AB,垂足为E,作半圆O的切线DC,交AB的延长线于点C,连结OD、BD.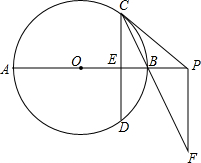 如图,已知AB是⊙O的直径,弦CD⊥AB于E,过C点的切线交AB的延长线于P,过P点作PF∥CD交CB的延长线于F.
如图,已知AB是⊙O的直径,弦CD⊥AB于E,过C点的切线交AB的延长线于P,过P点作PF∥CD交CB的延长线于F. 如图,直线a∥b,∠1=50°,∠2=30°,则∠3=20°.
如图,直线a∥b,∠1=50°,∠2=30°,则∠3=20°.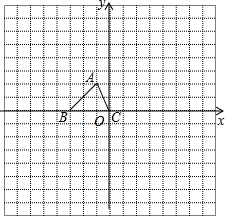 如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).
如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).