题目内容
18.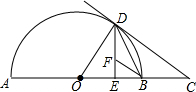 如图,AB是半圆O的直径,过半圆O上一点D作DE⊥AB,垂足为E,作半圆O的切线DC,交AB的延长线于点C,连结OD、BD.
如图,AB是半圆O的直径,过半圆O上一点D作DE⊥AB,垂足为E,作半圆O的切线DC,交AB的延长线于点C,连结OD、BD.(1)求证:BD平分∠CDE;
(2)过点B作BF∥CD交DE于点F,若BE=4,sin∠BOD=$\frac{4}{5}$,求线段BC的长.
分析 (1)由CD是⊙O的切线,得到∠CDB+∠ODB=90°,由DE⊥AB得到∠EDB+∠OBD=90°,然后根据等角的余角相等即可得到结论;
(2)由∠CDO=90°,sin∠BOD=$\frac{4}{5}$,设CD=4k,OC=5k由勾股定理得到OD=$\sqrt{O{C}^{2}-C{D}^{2}}$=3k,通过△COD∽△DOE,列比例式即可得到结论.
解答 (1)证明:∵CD是⊙O的切线,
∴∠CDO=90°,
∴∠CDB+∠ODB=90°,
∵DE⊥AB
∴∠DEB=90°,
∴∠EDB+∠OBD=90°,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠CDB=∠BDE,
∴BD平分∠CDE;
(2)解:∵∠CDO=90°,sin∠BOD=$\frac{4}{5}$,
∴设CD=4k,OC=5k,
∴OD=$\sqrt{O{C}^{2}-C{D}^{2}}$=3k,
∴OB=3k,BC=2k,
∵∠ODC=∠OED=90°,∠DOE=∠DOC,
∴△COD∽△DOE,
∴$\frac{OD}{OE}=\frac{OC}{OD}$,
∴OD2=OE•OC,
即(3k)2=(3k-4)•5k,
解得:k=$\frac{10}{3}$,
∴BC=2k=$\frac{20}{3}$.
点评 本题考查了切线的性质,角平分线的判定,三角函数,相似三角形的判定和性质,找准△COD∽△DOE是解题的关键.

练习册系列答案
相关题目
8.在开展“爱心捐助山区儿童”的活动中,某团小组8名团员捐款的数额分别为(单位:元):6,5,3,5,10,5,5,7.这组数据的中位数和众数分别是( )
| A. | 10,3 | B. | 6,5 | C. | 7,5 | D. | 5,5 |
6. 如图,从位于六和塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°.若此观测点离地面的高度CD为30米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,则A,B之间的距离为( )米.
如图,从位于六和塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°.若此观测点离地面的高度CD为30米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,则A,B之间的距离为( )米.
 如图,从位于六和塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°.若此观测点离地面的高度CD为30米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,则A,B之间的距离为( )米.
如图,从位于六和塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°.若此观测点离地面的高度CD为30米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,则A,B之间的距离为( )米.| A. | 30+10$\sqrt{3}$ | B. | 40$\sqrt{3}$ | C. | 45 | D. | 30+15$\sqrt{3}$ |
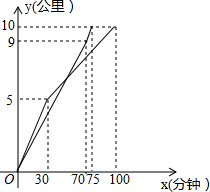 横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是$\frac{1}{6}$公里/分;(2)乙在冲刺阶段的速度$\frac{1}{5}$公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是$\frac{1}{6}$公里/分;(2)乙在冲刺阶段的速度$\frac{1}{5}$公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )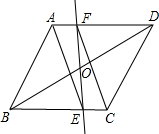 如图,在?ABCD中,O是对角线BD的中点,过O点的一条直线分别与BC相交于E,与AD相交于F,求证:四边形AECF是平行四边形.
如图,在?ABCD中,O是对角线BD的中点,过O点的一条直线分别与BC相交于E,与AD相交于F,求证:四边形AECF是平行四边形.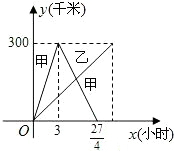 已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.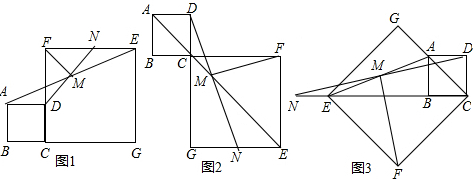
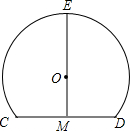 一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )
一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )