题目内容
10.如图,在平面直角坐标系中,点O为坐标原点,A点的坐标为(4,0),以OA为边作等边三角形OAB,点B在第一象限,过点B作AB的垂线交x轴于点C,动点P从O点出发沿OC向C点运动,动点Q从B点出发沿BA向A点运动.P,Q两点同时出发,P的速度是2个单位/秒,Q的速度是1个单位/秒.当一点到达终点时另一点也随之停止运动.(1)求线段BC的长:
(2)如图2,连接PQ交线段OB于点E,过点E作x轴的平行线交BC于点F,设线段EF的长为m,求m与t之间的函数关系式,并直接写出自变量的取值范围;
(3)在(2)的条件下,将△BEF绕点B逆时针旋转得到△BE′F′.使点E的对应点E′落在线段AB上,点F的对应点是F′,E′F′交x轴于点G.当QE′+GE′=3时,求t的值.

分析 (1)直接根据锐角三角函数的定义即可得出结论;
(2)根据等腰三角形的性质得出EF=EB,过点Q作QR∥PO,由相似三角形的性质得出$\frac{RE}{EO}$=$\frac{RO}{PO}$,故可用t表示出RO与RE的长,根据m=BR+RE即可得出结论;
(3)根据图形旋转的性质可知QE′=BE′-BQ,GE′=AE′=AB-BE′,再由QE′+GE′=3即可得出t的值.
解答  解:(1)∵在Rt△ABC中,AB=4,∠OAB=60°,
解:(1)∵在Rt△ABC中,AB=4,∠OAB=60°,
∴tan∠OAB=$\frac{BC}{AB}$=$\sqrt{3}$,
∴BC=4$\sqrt{3}$;
(2)∵∠BOA=60°,∠ABC=90°,
∴∠ACB=30°.
∵∠ABO=60°,
∴∠OBC=30°.
∵EF∥x轴,
∴∠BFE=∠ACB=∠OBC=30°,
∴EF=EB.
如图1,过点Q作QR∥PO,则∠RQE=∠OPE,
∵∠REQ=∠OEP,
∴△RQE∽△OPE,
∴$\frac{RE}{EO}$=$\frac{RO}{PO}$=$\frac{t}{2t}$=$\frac{1}{2}$,
∴RE=$\frac{1}{3}$RQ.
∵RO=4-t,
∴RE=$\frac{1}{3}$(4-t),
∴m=BR+RE=t+$\frac{4}{3}$-$\frac{t}{3}$=$\frac{2}{3}$t+$\frac{4}{3}$(0<t<2).
(3)如图2,QB=t,QE′=BE′-BQ=m-t=$\frac{2}{3}$t+$\frac{4}{3}$-t=-$\frac{1}{3}$t+$\frac{4}{3}$,GE′=AE′=AB-BE′=4-m=4-$\frac{2}{3}$t-$\frac{4}{3}$=-$\frac{2}{3}$t+$\frac{8}{3}$,
当QE′+GE′=3时,-$\frac{1}{3}$t+$\frac{4}{3}$-$\frac{2}{3}$t+$\frac{8}{3}$=3,解得t=1.
点评 本题考查的是相似形综合题,涉及到相似三角形的判定与性质、等边三角形及直角三角形的性质等知识,在解答(2)时,作出平行线,构造出相似三角形是解答此题的关键.

| A. | (2,3 ) | B. | (-2,-3) | C. | (-2,3) | D. | (-3,2) |
| A. | 6千米/小时 | B. | 8千米/小时 | C. | 9千米/小时 | D. | 15千米/小时 |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
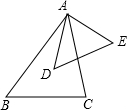 如图,若∠BAD=∠CAE,∠E=∠C,则△ABC∽△ADE.
如图,若∠BAD=∠CAE,∠E=∠C,则△ABC∽△ADE. 如图,两个正方形边长分别为a、b,如果a+b=18,ab=60,求图中阴影部分的面积.
如图,两个正方形边长分别为a、b,如果a+b=18,ab=60,求图中阴影部分的面积.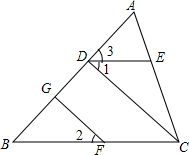 ∠1=∠2,∠3=∠B,FG⊥AB于G,猜想CD与AB的关系,并证明你的猜想.
∠1=∠2,∠3=∠B,FG⊥AB于G,猜想CD与AB的关系,并证明你的猜想.