Question

19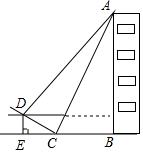．如图，我市某中学数学兴趣小组决定测量一下本校教学楼AB的高度，他们在楼梯底部C处测得∠ACB=60°，∠DCE=30°；沿楼梯向上走到D处测得∠ADF=45°，D到地面BE的距离DE为3米．求教学楼AB的高度．（站果精确列1米，参考数据：$\sqrt{2}≈$1.4，$\sqrt{3}$≈1.7）

Answer 1

分析 在Rt△DCE中求得CD=6，由∠ACD=90°、∠CDF=∠DCE=30°可得DF=$\frac{CD}{cos∠CDF}$=4$\sqrt{3}$，设AG=x，知DG=AG=x、FG=DG-DF=x-4$\sqrt{3}$，在Rt△AFG中，根据tan∠AFG=$\frac{AG}{FG}$求得x即可得出答案．

解答 解：如图，

在Rt△DCE中，∵∠DCE=30°、DE=3，
∴CD=2DE=6，
∵∠ACB=60°，
∴∠ACD=180°-∠DCE-∠ACB=90°，
∵∠CDF=∠DCE=30°，
∴在Rt△DCF中，DF=$\frac{CD}{cos∠CDF}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$，
设AG=x，
∵∠ADF=45°，
∴DG=AG=x，FG=DG-DF=x-4$\sqrt{3}$，
在Rt△AFG中，∵∠AFG=∠ACB=60°，
∴tan∠AFG=$\frac{AG}{FG}$，即$\frac{x}{x-4\sqrt{3}}$=$\sqrt{3}$，
解得：x=6+6$\sqrt{3}$，即AG=6+6$\sqrt{3}$，
∴AB=AG+BG=6+6$\sqrt{3}$+3=9+6$\sqrt{3}$≈19（米），
答：教学楼AB的高度约为19米．

点评 本题考查了解直角三角形的应用-仰角俯角问题，构造仰角所在的直角三角形，利用两个直角三角形的公共边求解是常用的解直角三角形的方法．