题目内容
19.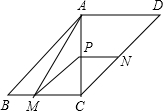 如图,在?ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发,沿AC向终点C移动,过点P分别作PM∥AB,交BC于M,PN∥AD,交DC于N.连结AM.
如图,在?ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发,沿AC向终点C移动,过点P分别作PM∥AB,交BC于M,PN∥AD,交DC于N.连结AM.(1)四边形PMCN的形状有可能是菱形吗?请说明理由;
(2)当AP=1时,四边形PMCN的面积与△ABM的面积是否相等?
分析 (1)由题可知,四边形PMCN是一个平行四边形,而要想成为一个菱形,则必须有邻边相等,如PM=MC,而PM和MC同在一直角三角形中,且PM为斜边>直角边MC,因此不会为菱形;
(2)在等腰直角△ABC中利用三角函数求得AC的长,则PC即可求得,从而求得CM的长,则△ABM和四边形PMCN的面积即可求得,即可作出判断.
解答 解:(1)四边形PMCN不可能是菱形.
点P在运动过程中,△PCM始终是一个直角三角形
斜边PM大于直角边MC
∴四边形PMCN不可能是菱形;
(2)在等腰直角△ABC中,AB=2,则AC=BC=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,
当AP=1时,PC=CM=$\sqrt{2}$-1.BM=2-($\sqrt{2}$-1)=3-$\sqrt{2}$.
则S△ABM=$\frac{1}{2}$BM•AC=$\frac{1}{2}$(3-$\sqrt{2}$)×$\sqrt{2}$=$\frac{3\sqrt{2}}{2}$-1.
S四边形PMCN=MC•PC=(3-$\sqrt{2}$)($\sqrt{2}$-1)=4$\sqrt{2}$-1.
则四边形PMCN的面积与△ABM的面积不相等.
点评 本题考查了菱形的判定与三角形的面积的计算,正确求得MC和PC的长是关键.

练习册系列答案
相关题目
7.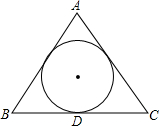 如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
 如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )| A. | 9$\sqrt{3}$ | B. | 18 | C. | 18$\sqrt{3}$ | D. | 54 |
9.如图,某建筑物由相同的若干个房间组成,该楼的三视图如图所示,试问:该楼有( )


| A. | 一层 | B. | 二层 | C. | 三层 | D. | 四层 |
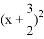 =
=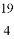 B.
B. 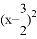 =
=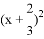 =
= =
=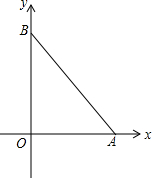 如图,在平面直角坐标系中,已知点A(3,0),点B(0,4),将线段AB绕点A按顺时针方向旋转得线段AB1,已知BB1和x轴平行.
如图,在平面直角坐标系中,已知点A(3,0),点B(0,4),将线段AB绕点A按顺时针方向旋转得线段AB1,已知BB1和x轴平行.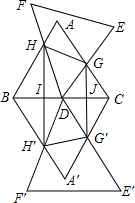 如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.
如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.