题目内容
10.若抛物线y=x2-mx-3与x轴分别交于A、B两点,且m为整数,则AB=4.分析 令x2-mx-3=0,则点A、B的横坐标为方程的根据,然后根据x1+x2=m且为整数,x1x2=-3可求得点A、B的横坐标,从而可求得AB的长.
解答 解:令y=0,得:x2-mx-3=0,
∵抛物线y=x2-mx-3与x轴分别交于A、B两点,且m为整数,
∴方程x2-mx-3=0的解为整数.
∵-1×3=-3,或1×(-3)=-3,
∴方程的两个为x1=-1,x2=3,或x1=1,x2=-3,
∴AB=3-(-1)=4或AB=1-(-3)=1+3=4.
故答案为4.
点评 本题主要考查的是抛物线与x轴的交点问题,根据题意求得点A、B的横坐标是解题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
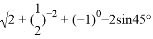
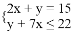 的x、y的正整数解。
的x、y的正整数解。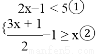 并把它的解集在数轴上表示出来.
并把它的解集在数轴上表示出来.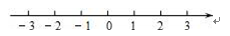
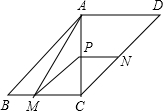 如图,在?ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发,沿AC向终点C移动,过点P分别作PM∥AB,交BC于M,PN∥AD,交DC于N.连结AM.
如图,在?ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发,沿AC向终点C移动,过点P分别作PM∥AB,交BC于M,PN∥AD,交DC于N.连结AM. 如图,在?ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD的度数为65°.
如图,在?ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD的度数为65°.