题目内容
7.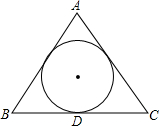 如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )| A. | 9$\sqrt{3}$ | B. | 18 | C. | 18$\sqrt{3}$ | D. | 54 |
分析 记△ABC的内切圆的圆心为O,连接OB、OD,先求得∠OBD和∠ODB的度数,然后依据勾股定理可求得BD的长,从而求得BC的长,最后可求得△ABC的周长.
解答 解:记△ABC的内切圆的圆心为O,连接OB、OD.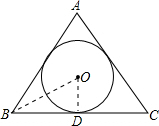
∵△ABC为等边三角形,
∴∠ABC=60°.
∵圆O为等边△ABC的内切圆,
∴∠OBD=$\frac{1}{2}$∠ABC=30°,OD⊥BD,BD=DC.
∴OB=2OD=6.
∴BD=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$.
∴BC=6$\sqrt{3}$.
∴△ABC的周长=3×6$\sqrt{3}$=18$\sqrt{3}$.
故选:C.
点评 本题主要考查的是三角形的内切圆,解答本题主要应用了等边三角形的性质、含30°直角三角形的性质、勾股定理、三角形的内心的性质,求得BD的长是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
17.无理数$\sqrt{12}-\sqrt{3}$的大小在以下两个整数之间( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |
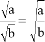 后,认为
后,认为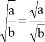 也成立,因此他认为一个化简过程:
也成立,因此他认为一个化简过程: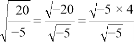
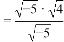 =
=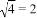 是正确的.你认为他的化简对吗?如果不对,请说明理由并改正.
是正确的.你认为他的化简对吗?如果不对,请说明理由并改正.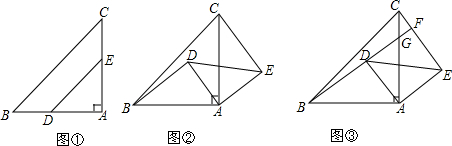
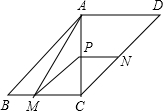 如图,在?ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发,沿AC向终点C移动,过点P分别作PM∥AB,交BC于M,PN∥AD,交DC于N.连结AM.
如图,在?ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发,沿AC向终点C移动,过点P分别作PM∥AB,交BC于M,PN∥AD,交DC于N.连结AM.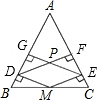 如图,在△ABC中,AB=AC,M是BC的中点,分别作MD⊥AB于D,ME⊥AC于E,DF⊥AC于F,EG⊥AB于G,DF、EG相交于点P,求证:四边形DMEP是菱形.
如图,在△ABC中,AB=AC,M是BC的中点,分别作MD⊥AB于D,ME⊥AC于E,DF⊥AC于F,EG⊥AB于G,DF、EG相交于点P,求证:四边形DMEP是菱形.