题目内容
在Rt△ABC中,∠C=90°,下列结论:(1)sinA<1;(2)若A>60°,则cosA>
;(3)若A>45°,则sinA>cosA.其中正确的有( )
| 1 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:锐角三角函数的增减性
专题:
分析:由Rt△ABC中,∠C=90°,根据三角形内角和定理可知∠A与∠B都是锐角,再根据特殊角的三角函数值及锐角三角函数的增减性即可求解.
解答:解:∵在Rt△ABC中,∠C=90°,
∴∠A与∠B都是锐角,
∴sinA<1,(1)正确;
∵cos60°=
,锐角余弦值随着角度的增大而减小,
∴若A>60°,则cosA<
,(2)错误;
∵cos(90°-A)=sinA,锐角正弦值随着角度的增大而增大,
∴若A>45°,则sinA>cosA,(3)正确.
故选C.
∴∠A与∠B都是锐角,
∴sinA<1,(1)正确;
∵cos60°=
| 1 |
| 2 |
∴若A>60°,则cosA<
| 1 |
| 2 |
∵cos(90°-A)=sinA,锐角正弦值随着角度的增大而增大,
∴若A>45°,则sinA>cosA,(3)正确.
故选C.
点评:本题主要考查了锐角三角函数的增减性,特殊角的三角函数值,是基础题,比较简单.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
根据下列表格对应值:
判断关于x的方程ax2+bx+c=0(x≠0)的一个解x的范围是( )
| x | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.02 | 0.01 | 0.03 |
| A、x<3.24 |
| B、3.24<x<3.25 |
| C、3.25<x<3.26 |
| D、3.25<x<3.28 |
若(2-x):x=x:(1-x),则x值为( )
| A、1 | ||
| B、±1 | ||
C、-
| ||
D、
|
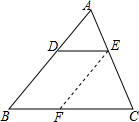 如图,在△ABC中,DE∥BC,DE分别交AB,AC于点D,E.
如图,在△ABC中,DE∥BC,DE分别交AB,AC于点D,E.