题目内容
根据下列表格对应值:
判断关于x的方程ax2+bx+c=0(x≠0)的一个解x的范围是( )
| x | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.02 | 0.01 | 0.03 |
| A、x<3.24 |
| B、3.24<x<3.25 |
| C、3.25<x<3.26 |
| D、3.25<x<3.28 |
考点:估算一元二次方程的近似解
专题:数形结合
分析:根据表中数据得到x=3.24时,ax2+bx+c=-0.02<0;x=3.25时,ax2+bx+c=0.01>0,于是可判断x在3.24和3.25之间取某一值时,ax2+bx+c=0,由此得到方程ax2+bx+c=0(x≠0)的一个解x的范围.
解答:解:∵x=3.24时,ax2+bx+c=-0.02<0;x=3.25时,ax2+bx+c=0.01>0,
∴当3.24<x<3.25时,ax2+bx+c的值可以等于0,
∴方程ax2+bx+c=0(x≠0)的一个解x的范围是3.24<x<3.25.
故选B.
∴当3.24<x<3.25时,ax2+bx+c的值可以等于0,
∴方程ax2+bx+c=0(x≠0)的一个解x的范围是3.24<x<3.25.
故选B.
点评:本题考查了估算一元二次方程的近似解:用列举法估算一元二次方程的近似解,具体方法是:给出一些未知数的值,计算方程两边结果,当两边结果愈接近时,说明未知数的值愈接近方程的根.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 下面的几何体是由哪个平面图形沿虚线旋转一周得到的( )
下面的几何体是由哪个平面图形沿虚线旋转一周得到的( )A、 |
B、 |
C、 |
D、 |
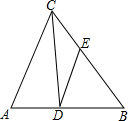 如图,在△ABC中,∠ACB的平分线交AB于点D,DE∥AC交BC于点E,若AC=9,CE=3,求BE的长.
如图,在△ABC中,∠ACB的平分线交AB于点D,DE∥AC交BC于点E,若AC=9,CE=3,求BE的长.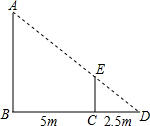 如图,身高为1.6m的小亮想测量一棵大树(AB)的高度,他沿着树影(BD)由点B向点D走动,当走到点C时,他的影子顶端正好与树的影子顶端重合(于点D),测得BC=5m,CD=2.5m,则树的高度为
如图,身高为1.6m的小亮想测量一棵大树(AB)的高度,他沿着树影(BD)由点B向点D走动,当走到点C时,他的影子顶端正好与树的影子顶端重合(于点D),测得BC=5m,CD=2.5m,则树的高度为


