题目内容
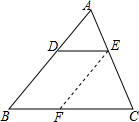如图，在△ABC中，DE∥BC，DE分别交AB，AC于点D，E．（1）△ADE与△ABC满足“对应角相等”吗？为什么？
（2）△ADE与△ABC满足对应边成比例吗？由DE∥BC的条件可得到哪些线段的比相等？
（3）根据以前学习的知识如何把DE移到BC上去？（作辅助线EF∥AB）你能证明AE：AC=DE：BC？从而得出△ABC∽△ADE．
考点：相似三角形的判定与性质
专题：
分析：（1）直接运用平行线的性质即可解决问题．
（2）根据相似三角形的判定及其性质即可解决问题．
（3）作辅助线，运用平行线分线段成比例定理，得到
=
，进而得到
=
，∠AED=∠C，问题即可解决．
（2）根据相似三角形的判定及其性质即可解决问题．
（3）作辅助线，运用平行线分线段成比例定理，得到
| AE |
| AC |
| BF |
| BC |
| AE |
| AC |
| DE |
| BC |
解答：解：（1）∵DE∥BC，
∴∠ADE=∠B，∠AED=∠C，而∠A=∠A，
∴△ADE与△ABC满足“对应角相等”．
（2）∵DE∥BC，
∴△ADE∽△ABC，
∴
=
=
．
∴△ADE与△ABC满足对应边成比例．
（3）
如图，过点E作EF∥AB，交BC于点F；
则四边形DBFE为平行四边形，
∴BF=DE；
∵EF∥AB，
∴
=
，
∴
=
，而∠AED=∠C，
∴△ABC∽△ADE．
解：（1）∵DE∥BC，∴∠ADE=∠B，∠AED=∠C，而∠A=∠A，
∴△ADE与△ABC满足“对应角相等”．
（2）∵DE∥BC，
∴△ADE∽△ABC，
∴
| AD |
| AB |
| AE |
| AC |
| DE |
| BC |
∴△ADE与△ABC满足对应边成比例．
（3）
如图，过点E作EF∥AB，交BC于点F；
则四边形DBFE为平行四边形，
∴BF=DE；
∵EF∥AB，
∴
| AE |
| AC |
| BF |
| BC |
∴
| AE |
| AC |
| DE |
| BC |
∴△ABC∽△ADE．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
相关题目
多项式
中，二次项的系数是（ ）
| -3x2+y |
| 4 |
| A、-3 | ||
| B、1 | ||
C、-
| ||
D、
|
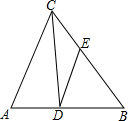如图，在△ABC中，∠ACB的平分线交AB于点D，DE∥AC交BC于点E，若AC=9，CE=3，求BE的长．
已知，如图，Rt△ACB中，∠ACB=90°，AC=kBC，P为AB上一点，作∠EPF=90°，分别交AC、CB的延长线于E、F两点．若PA=mPB，试判断PE、PF的数量关系，并说明理由．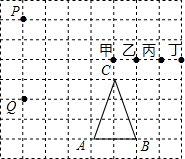
如图所示，若ABCPQ甲乙丙丁都是方格纸中的格点．如图，若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点，为使△PQR∽△ABC，则点R应是甲、乙、丙、丁四点中的（ ）
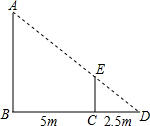如图，身高为1.6m的小亮想测量一棵大树（AB）的高度，他沿着树影（BD）由点B向点D走动，当走到点C时，他的影子顶端正好与树的影子顶端重合（于点D），测得BC=5m，CD=2.5m，则树的高度为