题目内容
若a-b=8,a2+b2=82,则ab= .
考点:完全平方公式
专题:
分析:由a-b=8可求出(a-b)2=a2+b2-2ab=64,将a2+b2=82代入该式中即可求出ab的值.
解答:解:∵a-b=8,
∴(a-b)2=a2+b2-2ab=64,
又∵a2+b2=82,
∴ab=9,
故答案是:9.
∴(a-b)2=a2+b2-2ab=64,
又∵a2+b2=82,
∴ab=9,
故答案是:9.
点评:本题主要考查完全平方公式的运用,熟练掌握两数和或差的平方,两数平方的和,两数乘积的二倍三者之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、有理数只是有限小数 | ||
| B、无理数是无限小数 | ||
| C、无限小数是无理数 | ||
D、-
|
一个三位数,个位、十位、百位上的数字分别是a、b、c,则这个三位数是( )
| A、cba |
| B、c+b+a |
| C、100c+10b+a |
| D、100abc |
下列运算正确的是( )
| A、(+8)+(-10)=-(10-8)=-2 |
| B、(-3)+(-2)=-(3-2)=-1 |
| C、(-5)+(+6)=+(6+5)=+11 |
| D、(-6)+(-2)=+(6+2)=+8 |
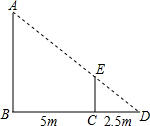 如图,身高为1.6m的小亮想测量一棵大树(AB)的高度,他沿着树影(BD)由点B向点D走动,当走到点C时,他的影子顶端正好与树的影子顶端重合(于点D),测得BC=5m,CD=2.5m,则树的高度为
如图,身高为1.6m的小亮想测量一棵大树(AB)的高度,他沿着树影(BD)由点B向点D走动,当走到点C时,他的影子顶端正好与树的影子顶端重合(于点D),测得BC=5m,CD=2.5m,则树的高度为