题目内容
 已知关于x的二次函数y=x2的图象与关于x的函数y=kx+1的图象交于两点A(x1,y1),B(x2,y2),(x1<x2),无论k为何值时,猜想△AOB的形状,证明你的猜想.
已知关于x的二次函数y=x2的图象与关于x的函数y=kx+1的图象交于两点A(x1,y1),B(x2,y2),(x1<x2),无论k为何值时,猜想△AOB的形状,证明你的猜想.考点:二次函数的性质
专题:
分析:当k为任意实数时,联立
,得x2-kx-1=0,根据一元二次方程根与系数的关系得到x1+x2=k,x1•x2=-1,根据两点间距离公式及完全平方公式求出AB2=k4+5k2+4,OA2+OB2=k4+5k2+4,由勾股定理的逆定理判定△AOB为直角三角形.
|
解答:解:猜想:△AOB为直角三角形.
∵
,得x2-kx-1=0,
∴x1+x2=k,x1•x2=-1,
∴AB2=(x1-x2)2+(y1-y2)2
=(x1-x2)2+(kx1-kx2)2
=(1+k2)(x1-x2)2
=(1+k2)[(x1+x2)2-4x1•x2]
=(1+k2)(4+k2)
=k4+5k2+4,
∵OA2+OB2=x12+y12+x22+y22
=x12+x22+y12+y22
=x12+x22+(kx1+1)2+(kx2+1)2
=x12+x22+(k2x12+2kx1+1)+(k2x22+2kx2+1)
=(1+k2)(x12+x22)+2k(x1+x2)+2
=(1+k2)(k2+2)+2k•k+2
=k4+5k2+4,
∴AB2=OA2+OB2,
∴△AOB为直角三角形.
∵
|
∴x1+x2=k,x1•x2=-1,
∴AB2=(x1-x2)2+(y1-y2)2
=(x1-x2)2+(kx1-kx2)2
=(1+k2)(x1-x2)2
=(1+k2)[(x1+x2)2-4x1•x2]
=(1+k2)(4+k2)
=k4+5k2+4,
∵OA2+OB2=x12+y12+x22+y22
=x12+x22+y12+y22
=x12+x22+(kx1+1)2+(kx2+1)2
=x12+x22+(k2x12+2kx1+1)+(k2x22+2kx2+1)
=(1+k2)(x12+x22)+2k(x1+x2)+2
=(1+k2)(k2+2)+2k•k+2
=k4+5k2+4,
∴AB2=OA2+OB2,
∴△AOB为直角三角形.
点评:本题考查的是二次函数的性质,其中涉及到的知识点有一次函数与二次函数的交点问题,勾股定理的逆定理等知识,有一定难度.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
如图所示,其中是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在等腰直角△ABC中,∠C=90°,O是斜边AB的中点,将直角三角板的直角顶点与点O重合,两直角边分别与边AC、BC交于点E、F,试判断AE与CF的数量关系,并进行证明.
如图,在等腰直角△ABC中,∠C=90°,O是斜边AB的中点,将直角三角板的直角顶点与点O重合,两直角边分别与边AC、BC交于点E、F,试判断AE与CF的数量关系,并进行证明.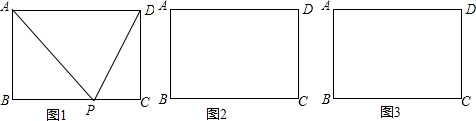
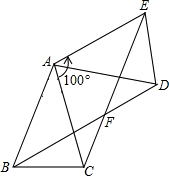 如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.
如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F. 如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图.
如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图.