题目内容
13.已知等腰△ABC三边分别为a,b,c,其中a=4,若关于x的一元二次方程x2-6x+b=0有两个相等的实数根.求等腰△ABC的周长.分析 若一元二次方程有两个相等的实数根,则根的判别式△=0,据此可求出b的值;进而可由三角形三边关系定理确定等腰三角形的三边长,即可求得其周长.
解答 解:∵关于x的方程x2-6x+b=0有两个相等的实数根,
∴△=62-4b=0,
解得b=9,
①当a为底,b为腰时,则9+9>4,能成三角形,
②当b为底,a为腰时,则4+4<9,不能够构成三角形;
此时△ABC的周长为:9+9+4=22,
答:△ABC的周长是22.
点评 此题考查了根与系数的关系、等腰三角形的性质及三角形三边关系定理;在求三角形的周长时,不能盲目的将三边相加,而应在三角形三边关系定理为前提条件下分类讨论,以免造成多解、错解.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | 4x-7x=3x | B. | 5a-3a=2 | C. | a2+a=a | D. | -2a-2a=-4a |
 如图,直线AC,DE相交于点O,OE是∠AOB的平分线,∠COD=50°.试求∠AOB的度数.
如图,直线AC,DE相交于点O,OE是∠AOB的平分线,∠COD=50°.试求∠AOB的度数.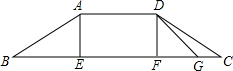 为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=10$\sqrt{5}$米,tanB=$\frac{1}{2}$,∠C=30°.
为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=10$\sqrt{5}$米,tanB=$\frac{1}{2}$,∠C=30°.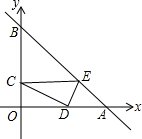 如图,点A的坐标是(4,0),B的坐标是(0,4),点C在射线OB上,过点C作CE∥x轴交直线AB于点E,D为x轴正半轴上的一点,OD=2OC,连接CD,DE,设OC=m.
如图,点A的坐标是(4,0),B的坐标是(0,4),点C在射线OB上,过点C作CE∥x轴交直线AB于点E,D为x轴正半轴上的一点,OD=2OC,连接CD,DE,设OC=m. 如图,DE∥AB,FG∥BC,HM∥CA,求∠D+∠E+∠F+∠G+∠H+∠M的度数.
如图,DE∥AB,FG∥BC,HM∥CA,求∠D+∠E+∠F+∠G+∠H+∠M的度数.