题目内容
2．
如图，DE∥AB，FG∥BC，HM∥CA，求∠D+∠E+∠F+∠G+∠H+∠M的度数．
分析 根据平行线的性质得到∠D=∠BAC，∠AFG=∠E，∠AFG=∠B，∠AGF=∠C，∠M=∠BAC，∠H=∠AGF，根据三角形的内角和定理和等量代换即可得到结论．
解答 解：∵DE∥AB，
∴∠D=∠BAC，∠AFG=∠E，
∵FG∥BC，
∴∠AFG=∠B，∠AGF=∠C，
∵HM∥CA，
∴∠M=∠BAC，∠H=∠AGF，
∴∠D+∠E+∠F+∠G+∠H+∠M=2（∠BAC+∠B+∠C）=360°．
点评 本题考查了平行线的性质，三角形的内角和，熟练掌握平行线的性质是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
对于每个关于x的函数，y是y1=x+2，y2=$\frac{4}{x}$（x＞0），y3=x2-5x+7这三个函数中的最小值，这三个函数的图象如图所示，则函数y的最大值是3．
图中共有射线7条，线段有6条．
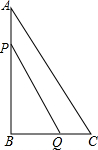如图，在△ABC中，∠B=90°，AB=8cm，BC=6cm，点P从点A开始沿AB边以1cm/秒向点B速度移动，点Q从点B开始沿BC边以2cm/秒的速度向点C移动，当Q点到达C点时，P，Q停止移动，如果P，Q分别从A，B同时出发；
如图，△ABC中，∠C=90°，AD是∠CAB的平分线，DE⊥AB，垂足为E，若AD=10，AC=8，则DE的长是6．