题目内容
8.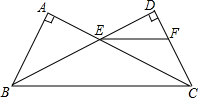 已知:如图,AB=DC,∠A=∠D=90°,AC,BD相交于点E,EF∥BC交CD于点F.求证:EF平分∠DEC.
已知:如图,AB=DC,∠A=∠D=90°,AC,BD相交于点E,EF∥BC交CD于点F.求证:EF平分∠DEC.
分析 先证明△ABE≌△DCE得BE=EC得∠EBC=∠ECB,再由EF∥BC得∠DEF=∠EBC,∠FEC=∠ECB即可证明.
解答  证明:在△ABE和△DCE中,
证明:在△ABE和△DCE中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠AEB=∠DEC}\\{AB=DC}\end{array}\right.$,
∴△ABE≌△DCE,
∴BE=EC,
∴∠EBC=∠ECB,
∵EF∥BC,
∴∠DEF=∠EBC,∠FEC=∠ECB,
∴∠DEF=∠FEC,
∴EF平分∠DEC.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质、平行线的性质,寻找全等三角形是解决问题的关键.

练习册系列答案
相关题目
8.据武汉大学互联网科学研究中心统计,从3月3日零时至3月8日17时,两会相关微博讨论量为3162200条,3162200用科学记数法表示为( )
| A. | 3.1622×107 | B. | 0.31622×107 | C. | 3.1622×106 | D. | 31.622×105 |
9.已知从小到大排列的一组数据2,3,4,x1,x2,x3的中位数和平均数是8,那么4x1-(x2+x3)的值是( )
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
18.在某市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生的读书情况,随机调查了八年级50名学生读书的册数,统计数据如表所示:
①求这50名学生读书册数的平均数,众数和中位数;
②估计该校八年级在本次活动中读书多于2册的学生人数占全年级的百分比.
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
②估计该校八年级在本次活动中读书多于2册的学生人数占全年级的百分比.
 如图,在△ABC中,∠ABC=60°,∠BAC、∠BCA的平分线相交于点O,求证:OE=OF.
如图,在△ABC中,∠ABC=60°,∠BAC、∠BCA的平分线相交于点O,求证:OE=OF. 如图,一只蜘蛛在一个正方形框架(每个方格都是正方向)的A处,一只苍蝇在这个正方形框架的B处,这只蜘蛛要袭击这只苍蝇(它必须沿正方形框架线路爬行).那么它袭击苍蝇的最佳路线有6条.
如图,一只蜘蛛在一个正方形框架(每个方格都是正方向)的A处,一只苍蝇在这个正方形框架的B处,这只蜘蛛要袭击这只苍蝇(它必须沿正方形框架线路爬行).那么它袭击苍蝇的最佳路线有6条. 如图所示,a⊥b,b∥c,∠1=120°,则∠2的度数是30°.
如图所示,a⊥b,b∥c,∠1=120°,则∠2的度数是30°.