题目内容
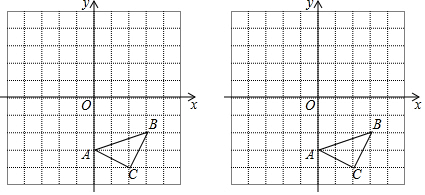
9.如图,在?ABCD中,点E,F分别为边BC,AD的中点,连接AE,CF.(1)如图1,求证:四边形AECF是平行四边形;
(2)如图2,过点D作DG⊥AB,垂足为点G,若AG=AB,请直接写出图2中所有与CF相等的线段(不包括CF)

分析 (1)只要证明AF=EC,AF∥EC即可;
(2)如图2中,连接AC.首先证明四边形AGDC是矩形.推出∠ACD=∠GAC=∠BAC=90°由AF=DF,BE=EC,可得CF=AF=DF,AE=BE=CE;
解答 解:(1)如图1中,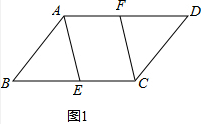
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E,F分别为边BC,AD的中点,
∴CE=$\frac{1}{2}$BC,AF=$\frac{1}{2}$AD,
∴AF=EC,AF∥CE,
∴四边形AECF是平行四边形.
(2)如图2中,连接AC..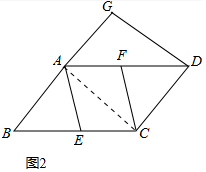
∵AG=AB=CD,AG∥CD,
∴四边形AGDC是矩形,
∵∠G=90°,
∴四边形AGDC是矩形.
∴∠ACD=∠GAC=∠BAC=90°
∵AF=DF,BE=EC,
∴CF=AF=DF,AE=BE=CE,
∴与CF相等的相等有AF,DF,BE,CE,AE.
点评 本题考查平行四边形的判定和性质、矩形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
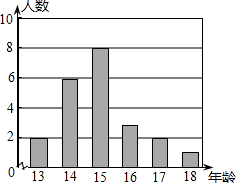 某校男子足球队队员的年龄分布为如图的条形图,则这些队员年龄的众数、中位数分别是15,15.
某校男子足球队队员的年龄分布为如图的条形图,则这些队员年龄的众数、中位数分别是15,15.
 如图,直线AB,CD被直线EF所截,EG平分∠BEF交CD于G,∠1=∠2=58°,求∠EGF的度数.
如图,直线AB,CD被直线EF所截,EG平分∠BEF交CD于G,∠1=∠2=58°,求∠EGF的度数.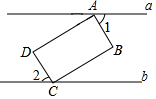 如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=66°,则∠2的度数为?
如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=66°,则∠2的度数为?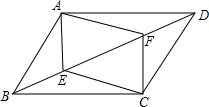 如图:在?ABCD中,E、F分别为对角线BD上的点,且BE=DF,判断四边形AECF的形状,并说明理由.
如图:在?ABCD中,E、F分别为对角线BD上的点,且BE=DF,判断四边形AECF的形状,并说明理由.