题目内容
18.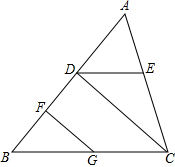 如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.
如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.解:∵∠ADE=∠B(已知)
∴DE∥BC同位角相等,两直线平行
∴∠EDC=∠DCB两直线平行,内错角相等
∵∠EDC=∠FGB(已知)
∴∠DCB=∠FGB(等量代换)
∴FG∥DC (同位角相等,两直线平行)
∴∠CDB=∠FGB两直线平行,同位角相等
∵GF⊥AB已知
∴∠GFB=90°(垂线的定义)
∴∠CDB=90°等量代换
∴CD⊥AB垂线的定义.
分析 根据平行线的性质与判定定理即可作出解决.
解答 解:∵∠ADE=∠B(已知),
∴DE∥BC (同位角相等,两直线平行)
∴∠EDC=∠DCB (两直线平行,内错角相等),
∵∠EDC=∠FGB(已知),
∴∠DCB=∠FGB(等量代换),
∴FG∥DC (同位角相等,两直线平行),
∴∠CDB=∠FGB (两直线平行,同位角相等),
∵GF⊥AB (已知),
∴∠GFB=90°(垂线的定义),
∴∠CDB=90°(等量代换),
∴CD⊥AB (垂线的定义).
故答案为:(同位角相等,两直线平行),(两直线平行,内错角相等),(两直线平行,同位角相等),(已知),(等量代换),(垂线的定义).
点评 本题考查了平行线的性质定理以及判定定理,关键性质定理与判定定理二者之间的区别以及正确掌握同位角、内错角、同旁内角的定义.

练习册系列答案
相关题目
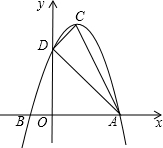 如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.
如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.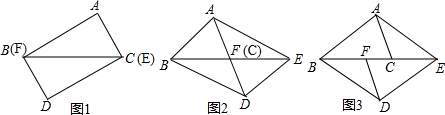
 如图,已知直线y=kx-3经过点M,求此直线的函数关系式,并求与x轴、y轴的交点坐标.
如图,已知直线y=kx-3经过点M,求此直线的函数关系式,并求与x轴、y轴的交点坐标. 已知△ABC,求作△ABC的三边的垂直平分线.(只用直尺和圆规)
已知△ABC,求作△ABC的三边的垂直平分线.(只用直尺和圆规)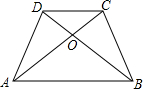 如图,AD=BC,AC=BD,AC与BD相交于O点,则图中全等三角形共有3对.
如图,AD=BC,AC=BD,AC与BD相交于O点,则图中全等三角形共有3对.