题目内容
8.方程组$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=-3}\end{array}\right.$的解为$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$.分析 把c的值代入前两个方程,然后解关于a、b的方程组.
解答 解:由原方程组,得
$\left\{\begin{array}{l}{a-b=3①}\\{3a+b=1②}\end{array}\right.$,
由①+②,得
4a=4,
解得a=1.
把a=1代入①,得
1-b=3,则b=-2,
所以原方程组的解为:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$,
故答案是:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$.
点评 本题考查了解三元一次方程组的解法,有加减法和代入法两种,一般选用加减法解二元一次方程组较简单.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
19.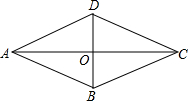 如图,在菱形ABCD中,对角线AC、BD交于点O,下列说法错误的是( )
如图,在菱形ABCD中,对角线AC、BD交于点O,下列说法错误的是( )
 如图,在菱形ABCD中,对角线AC、BD交于点O,下列说法错误的是( )
如图,在菱形ABCD中,对角线AC、BD交于点O,下列说法错误的是( )| A. | AD∥BC | B. | OA=OC | C. | AC⊥BD | D. | AC=BD |
16.2013年10月,雾霾天气笼罩中国中东部大部分地区,北京及全国多个城市PM2.5严重超标,多地空气质量达严重污染,环境治理已成为民生中的热点问题,小强为了了解本市空气质量情况,从“中国环境保护网”数据中心查询到本市2013年全年的空气质量级别资料,用简单随机抽样的方法选取60天,并得出如下所示的统计表和扇形统计图:
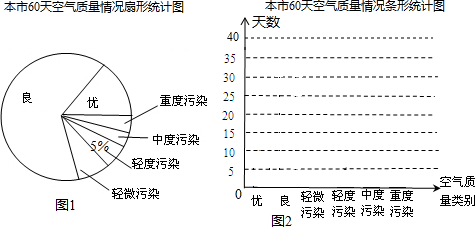
请你根据所给信息解答下列问题:
(1)求a,b的值;
(2)这次抽样中,“空气质量不低于良”的频率为$\frac{4}{5}$;
(3)画出本市60天空气质量情况条形统计图;
(4)根据这次抽样结果,请你估计2013年全年(共365天)空气质量为优良的天数是多少?
| 空气质量级别 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 10 | a | 4 | b | 3 | 2 |

请你根据所给信息解答下列问题:
(1)求a,b的值;
(2)这次抽样中,“空气质量不低于良”的频率为$\frac{4}{5}$;
(3)画出本市60天空气质量情况条形统计图;
(4)根据这次抽样结果,请你估计2013年全年(共365天)空气质量为优良的天数是多少?
13.已知一组数据的最大值为46,最小值为27,在绘制频数分布直方图时,取组距为3,则这组数据应分成( )
| A. | 5组 | B. | 6组 | C. | 7组 | D. | 8组 |
20.下列调查适合用抽样调查的是( )
| A. | 了解中央电视台“成语大赛”节目的收视率 | |
| B. | 了解某班每个学生的体育达标情况 | |
| C. | 了解某班每个学生家庭电脑的数量 | |
| D. | “辽宁号”航母下海之前对重要零部件的检查 |
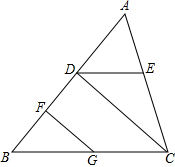 如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.
如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.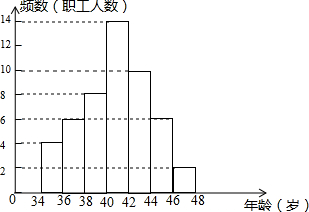 如图是某单位职工年龄(取正整数)的频数分布直方图(每组数据含最小值,不含最大值).
如图是某单位职工年龄(取正整数)的频数分布直方图(每组数据含最小值,不含最大值).