题目内容
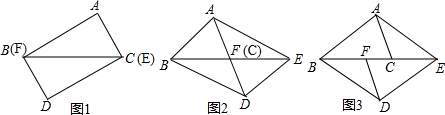
13.在手工制作活动课上,小明剪了两个全等的△ABC和△DEF.(1)若把△ABC和△DEF如图1放置,则四边形ABDC是平行四边形,并说明理由;
(2)若把△DEF沿直线BC向右平移到如图2位置,连接AE、BD,四边形ABDE是平行四边形吗?说明理由;
(3)若把△DEF沿直线BC向右平移到如图3位置,连接AE、BD,四边形ABDE是平行四边形吗?(回答:“是”或“不是”,不必说明理由)
分析 (1)由全等三角形的性质得出AB=DE,AC=DF,由平行四边形的判定定理即可得出结论;
(2)由平移和全等三角形的性质得出AC=DF,BC=EF,由平行四边形的判定定理即可得出结论;
(3)由平移和全等三角形的性质得出AB∥DE,AB=DE,由平行四边形的判定定理即可得出结论.
解答 解:(1)四边形ABDC是平行四边形;理由如下:
∵△ABC≌△DEF,
∴AB=DE,AC=DF,
∴四边形ABDC是平行四边形(两组对边分别相等的四边形是平行四边形);
故答案为:平行四边形;
(2)四边形ABDE是平行四边形;理由如下:
根据题意得:F(C)是四边形ABDE对角线的交点,
∵△ABC≌△DEF,
∴AC=DF,BC=EF,
∴四边形ABDE是平行四边形(对角线互相平分的四边形是平行四边形);
(3)是;理由:
由平移的性质得:AB∥DE,
又∵AB=DE,
∴四边形ABDE是平行四边形(一组对边平行且相等的四边形是平行四边形).
点评 本题考查了平行四边形的判定定理、全等三角形的性质、平移的性质;熟练掌握全等三角形的性质和平行四边形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 如图,O为平行四边形ABCD对角线的交点,DE∥AC,CE∥BD,CE=DE,求证:四边形ABCD为矩形.
如图,O为平行四边形ABCD对角线的交点,DE∥AC,CE∥BD,CE=DE,求证:四边形ABCD为矩形.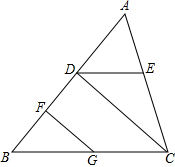 如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.
如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.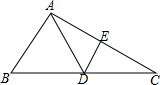 如图,在△ABC中,AC的垂直平分线交BC于点D,△ABD的周长为13,AE=3,则△ABC的周长为19.
如图,在△ABC中,AC的垂直平分线交BC于点D,△ABD的周长为13,AE=3,则△ABC的周长为19.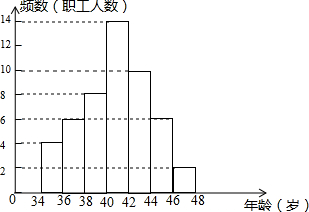 如图是某单位职工年龄(取正整数)的频数分布直方图(每组数据含最小值,不含最大值).
如图是某单位职工年龄(取正整数)的频数分布直方图(每组数据含最小值,不含最大值).