题目内容
16.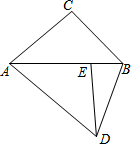 如图,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连结BD,如果∠DAC=∠DBA,那么∠BAC度数是36度.
如图,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连结BD,如果∠DAC=∠DBA,那么∠BAC度数是36度.
分析 设∠BAC=x,依据旋转的性质,可得∠DAE=∠BAC=x,∠ADB=∠ABD=2x,再根据三角形内角和定理即可得出x.
解答 解:设∠BAC=x,由旋转的性质,可得
∠DAE=∠BAC=x,
∴∠DAC=∠DBA=2x,
又∵AB=AD,
∴∠ADB=∠ABD=2x,
又∵△ABD中,∠BAD+∠ABD+∠ADB=180°,
∴x+2x+2x=180°,
∴x=36°,
即∠BAC=36°,
故答案为:36
点评 本题主要考查了旋转的性质以及三角形内角和定理,解题时注意:旋转前、后的图形全等.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
7.计算$\sqrt{27}$-$\sqrt{8}$•$\sqrt{\frac{2}{3}}$的结果是( )
| A. | $\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{3}$ | C. | $\frac{5}{3}\sqrt{3}$ | D. | $2\sqrt{3}$ |
11. 将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
 将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )| A. | 136° | B. | 138° | C. | 140° | D. | 142° |
 如图,正五边形的边长为2,连对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,则MN=3-$\sqrt{5}$.
如图,正五边形的边长为2,连对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,则MN=3-$\sqrt{5}$. 如图,直线l1∥l2,CD⊥AB于点D,∠1=44°,则∠2的度数为46°.
如图,直线l1∥l2,CD⊥AB于点D,∠1=44°,则∠2的度数为46°.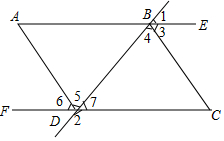 如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠FDB,试问∠3与∠4有怎样的数量关系,并说明理由.
如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠FDB,试问∠3与∠4有怎样的数量关系,并说明理由.