题目内容
7.下列说法正确的是( )| A. | (-3)2的算术平方根是3 | B. | $\sqrt{225}$的平方根是±15 | ||
| C. | 当x=0或2时,x$\sqrt{x-2}$=0 | D. | $\frac{\sqrt{3}}{2}$是分数 |
分析 根据算术平方根、平方根的性质、分数的定义,可得答案.
解答 解:A、(-3)2的算术平方根是3,故选项正确;
B、$\sqrt{225}$的平方根是±$\sqrt{15}$,故选项错误;
C、当x=0时,x$\sqrt{x-2}$=无意义,故选项错误;
D、$\frac{\sqrt{3}}{2}$是无理数,故选项错误.
故选:A.
点评 本题考查了实数,利用算术平方根、平方根的性质、分数的定义是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.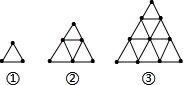 探索规律并填空
探索规律并填空
1+2=$\frac{2×(1+2)}{2}$;
1+2+3=$\frac{3×(1+3)}{2}$;
1+2+3+4=$\frac{4×(1+4)}{2}$;
1+2+3…+20=210;
1+2+3+…+n=$\frac{n(n+1)}{2}$.
用火柴棒按下面的方式搭图形填写表
照规律搭下去:
(1)第n个图形的大三角形周长的火柴棒是几根?
(2)第n个图形的小三角形个数有几个?第200个图形的小三角形个数有几个?
 探索规律并填空
探索规律并填空1+2=$\frac{2×(1+2)}{2}$;
1+2+3=$\frac{3×(1+3)}{2}$;
1+2+3+4=$\frac{4×(1+4)}{2}$;
1+2+3…+20=210;
1+2+3+…+n=$\frac{n(n+1)}{2}$.
用火柴棒按下面的方式搭图形填写表
| 图形编号 | ① | ② | ③ | ④ |
| 大三角形周长的火柴棒根数 | 3 | 6 | 9 | 12 |
| 小三角形个数 | 1 | 4 | 9 | 16 |
(1)第n个图形的大三角形周长的火柴棒是几根?
(2)第n个图形的小三角形个数有几个?第200个图形的小三角形个数有几个?
2.下列图形中,∠1和∠2是内错角的是( )
| A. | 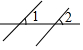 | B. | 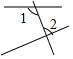 | C. | 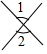 | D. | 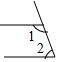 |
 如图,直线l1∥l2,CD⊥AB于点D,∠1=44°,则∠2的度数为46°.
如图,直线l1∥l2,CD⊥AB于点D,∠1=44°,则∠2的度数为46°.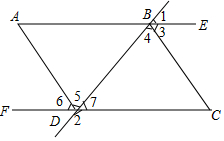 如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠FDB,试问∠3与∠4有怎样的数量关系,并说明理由.
如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠FDB,试问∠3与∠4有怎样的数量关系,并说明理由. 如图,⊙O是等边△ABC的外接圆,M是BC延长线上一点,连接AM交⊙O于点D,延长BD至点N,使得BN=AM,连接CN,MN.
如图,⊙O是等边△ABC的外接圆,M是BC延长线上一点,连接AM交⊙O于点D,延长BD至点N,使得BN=AM,连接CN,MN.