题目内容
4．
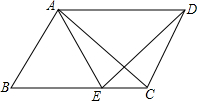如图所示，在平行四边形ABCD中，E为BC边上一点，且AB=AE，求证：△ABC≌△EAD．
分析 根据平行四边形的性质可得∠DAE=∠AEB，AD=BC，再证明∠B=∠DAE，然后可利用SAS定理证明△ABC≌△EAD．
解答 证明：∵四边形ABCD是平行四边形，
∴∠DAE=∠AEB，AD=BC，
∵AB=AE，
∴∠B=∠AEB，
∴∠B=∠DAE，
在△ABC和△EAD中，
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠EAD}\\{CB=AD}\end{array}\right.$，
∴△ABC≌△EAD（SAS）．
点评 此题主要考查了平行四边形的性质和全等三角形的判定，关键是掌握判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
练习册系列答案
相关题目
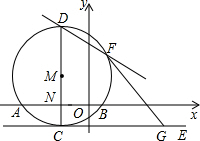如图，⊙M与x轴交于A、B两点，其坐标分别为A（-3，0）、B（1，0），直径CD⊥x轴于N，抛物线y=-x2-2x+m经过A、B、D三点，
如图，在平行四边形ABCD中，E，F分别是AB，CD的中点，若AD⊥BD，问四边形BEDF是什么特殊的四边形？
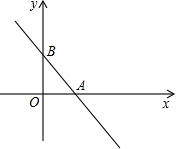已知：一次函数y=-$\frac{4}{3}$x+4的函数与x轴、y轴交于A、B两点．
如图，点D为△ABC的边BC上的一点，且∠ADC=∠ACD．证明：∠ACB＞∠B．