题目内容
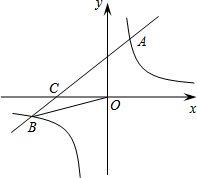 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=| k |
| x |
| 2 |
| 5 |
(1)求该反比例函数和一次函数的解析式,并写出使y1<y2成立的x的取值范围;
(2)若M是直线AB上一点,使得△MBO∽△OBC,求点M的坐标.
考点:反比例函数综合题
专题:
分析:(1)先过点B作BD⊥x轴,根据已知求出点B的坐标,再代入反比例函数y2=
(k≠0)的中,求出反比例函数的解析式,从而求出点A的坐标,再把点A、点B的坐标代入y1=ax+b,求出一次函数的解析式,再根据y1与y2交于(2,5)(-5,-2),求出x的取值范围;
(2)过点B作BD⊥x轴于点D,根据点B的坐标求出OB和BC的值,若△MBO∽△OBC,得出
=
,求出MD的值,设M的坐标为(t,t+3),求出t的值,即可得出答案.
| k |
| x |
(2)过点B作BD⊥x轴于点D,根据点B的坐标求出OB和BC的值,若△MBO∽△OBC,得出
| MD |
| DC |
| BO |
| BC |
解答: 解:(1)过点B作BD⊥x轴,
解:(1)过点B作BD⊥x轴,
∵tan∠BOC=
,
∴
=
,
∴n=-5,
∴点B的坐标是(-5,-2),
∴反比例函数的解析式为:y2=
;
∴点A的坐标是(2,5),
把(2,5)(-5,-2)代入y1=ax+b得:
,
解得:
,
∴一次函数的解析式为;y1=x+3,
∵y1与y2交于(2,5)(-5,-2),
∴当y1<y2时,x的取值范围是x<-5或0<x<2;
(2)过点B作BD⊥x轴于点D,
∵点B的坐标为(-5,-2),
∴OB=
=
,BC=
=2
,
若△MBO∽△OBC,
则
=
,
∴
=
,
∴MD=
,
设M的坐标为(t,t+3),
∴t2+(t+3)2=(
)2,
解得:t1=
,t2=-
(舍去),
∴M的坐标为(
,
).
 解:(1)过点B作BD⊥x轴,
解:(1)过点B作BD⊥x轴,∵tan∠BOC=
| 2 |
| 5 |
∴
| 2 |
| -n |
| 2 |
| 5 |
∴n=-5,
∴点B的坐标是(-5,-2),
∴反比例函数的解析式为:y2=
| 10 |
| x |
∴点A的坐标是(2,5),
把(2,5)(-5,-2)代入y1=ax+b得:
|
解得:
|
∴一次函数的解析式为;y1=x+3,
∵y1与y2交于(2,5)(-5,-2),
∴当y1<y2时,x的取值范围是x<-5或0<x<2;
(2)过点B作BD⊥x轴于点D,
∵点B的坐标为(-5,-2),
∴OB=
| 22+52 |
| 29 |
| 22+22 |
| 2 |
若△MBO∽△OBC,
则
| MD |
| DC |
| BO |
| BC |
∴
| MD |
| 3 |
| ||
2
|
∴MD=
3
| ||
| 4 |
设M的坐标为(t,t+3),
∴t2+(t+3)2=(
3
| ||
| 4 |
解得:t1=
| 9 |
| 4 |
| 21 |
| 4 |
∴M的坐标为(
| 9 |
| 4 |
| 21 |
| 4 |
点评:此题考查了反比例函数的综合,用到的知识点是函数解析式的求法、相似三角形的性质、勾股定理等,注意把不合题意的值舍去.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 如图,在△ABC中,AB=AC,AD平分∠BAC,那么下列结论不一定成立的是( )
如图,在△ABC中,AB=AC,AD平分∠BAC,那么下列结论不一定成立的是( )| A、△ABD≌△ACD |
| B、AD是△ABC的高线 |
| C、AD是△ABC的角平分线 |
| D、△ABC是等边三角形 |
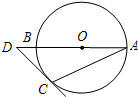 如图,AB是⊙0的直径,点D在AB的延长线上,过点D作⊙0的切线,切点为C,若∠A=25°,则∠D=( )
如图,AB是⊙0的直径,点D在AB的延长线上,过点D作⊙0的切线,切点为C,若∠A=25°,则∠D=( )| A、60° | B、65° |
| C、50° | D、40° |
 如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为
如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为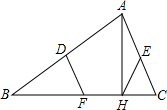 已知:如图,D、E、F分别是△ABC三边中点,AH⊥BC于H,求证:DF=EH.
已知:如图,D、E、F分别是△ABC三边中点,AH⊥BC于H,求证:DF=EH.