题目内容
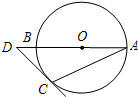 如图,AB是⊙0的直径,点D在AB的延长线上,过点D作⊙0的切线,切点为C,若∠A=25°,则∠D=( )
如图,AB是⊙0的直径,点D在AB的延长线上,过点D作⊙0的切线,切点为C,若∠A=25°,则∠D=( )| A、60° | B、65° |
| C、50° | D、40° |
考点:切线的性质
专题:
分析:连接OC,先根据圆周角定理得∠DOC=2∠A=40°,再根据切线的性质定理得∠OCD=90°,则此题易解.
解答: 解:连接OC,
解:连接OC,
∵∠A=25°,
∴∠DOC=2∠A=50°,
又∵∠OCD=90°,
∴∠D=40°.
故选:D.
 解:连接OC,
解:连接OC,∵∠A=25°,
∴∠DOC=2∠A=50°,
又∵∠OCD=90°,
∴∠D=40°.
故选:D.
点评:此题综合运用了切线的性质定理、圆周角定理和直角三角形的两个锐角互余的性质.

练习册系列答案
相关题目
下列方程是一元二次方程的是( )
| A、3x2-6x+2 | ||
| B、x2-y+1=0 | ||
| C、x2=0 | ||
D、
|
在下列长度的各组线段中,能构成直角三角形的是( )
| A、3,5,9 | ||||||
B、1,
| ||||||
| C、4,6,8 | ||||||
D、
|
定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“凤凰”方程.已知方程a1x2+b1x+c1=0(a≠0)是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
| A、a1=b1 |
| B、a1=c1 |
| C、b1=c1 |
| D、a1=b1=c1 |
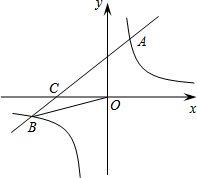 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2= 如图,Rt△ABC中∠C=90°,D在BC上,AB⊥BE,EF⊥BC于F,∠EAB=∠DAC.求证:
如图,Rt△ABC中∠C=90°,D在BC上,AB⊥BE,EF⊥BC于F,∠EAB=∠DAC.求证: